题目内容

已知cosx=-
4
5
，且x∈(π，
3
2
π)，则tanx等于（　　）
分析：由x的范围判断出sinx的值小于0，由cosx的值，利用同角三角函数间的平方关系求出sinx的值，再弦化切即可求出tanx的值．
解答：解：∵cosx=-
4
5
，x∈(π，
3
2
π)
sinx=-
1-(-
4
5
)
2=-
3
5

∴tanx=
sinx
cosx
=
-
3
5
-
4
5
=
3
4

故选：C．
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
（1）计算：tan(-
23π
6
)；（4分）
（2）已知cosx=-
4
5
，且x∈(-π，-
π
2
)，求tanx得值．（4分）
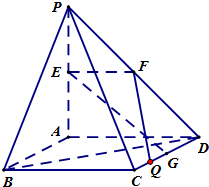精英家教网（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（1）求异面直线EG与BD所成角的大小；
（2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为
4
5
？若存在，求出线段CQ的长；若不存在，请说明理由．
（文）已知坐标平面内的一组基向量为
e
1=(1，sinx)，
e
2=(0，cosx)，其中x∈[0，
π
2
)，且向量
a
=
1
2
e
1+
3
2
e
2．
（1）当
e
1和
e
2都为单位向量时，求|
a
|；
（2）若向量
a
和向量
b
=(1，2)共线，求向量
e
1和
e
2的夹角．
（1）计算：tan(-
23π
6
)；（4分）
（2）已知cosx=-
4
5
，且x∈(-π，-
π
2
)，求tanx得值．（4分）
已知cosx=-
4
5
，且x∈(π，
3
2
π)，则tanx等于（　　）
A．-
3
4
B．-
4
3
C．
3
4
D．
4
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网