题目内容
(本小题满分14分)已知函数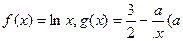 为实常数).
为实常数).
(I)当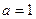 时,求函数
时,求函数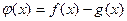 在
在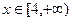 上的最小值;
上的最小值;
(Ⅱ)若方程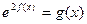 (其中
(其中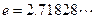 )在区间
)在区间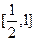 上有解,求实数
上有解,求实数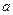 的取值范围;
的取值范围;
(Ⅲ)证明: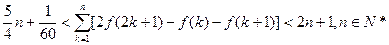 (参考数据:
(参考数据: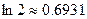 )
)
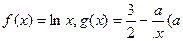 为实常数).
为实常数).(I)当
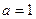 时,求函数
时,求函数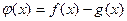 在
在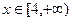 上的最小值;
上的最小值;(Ⅱ)若方程
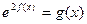 (其中
(其中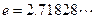 )在区间
)在区间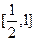 上有解,求实数
上有解,求实数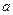 的取值范围;
的取值范围;(Ⅲ)证明:
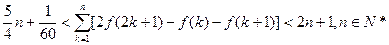 (参考数据:
(参考数据: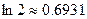 )
)(I)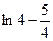 ;(Ⅱ)
;(Ⅱ)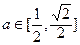 ;(Ⅲ) (略).
;(Ⅲ) (略).
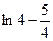 ;(Ⅱ)
;(Ⅱ)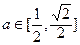 ;(Ⅲ) (略).
;(Ⅲ) (略).(Ⅰ)当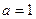 时,
时,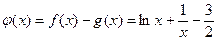 ,
,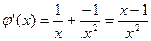 ,令
,令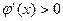 ,又
,又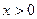 ,
,
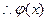 在
在 上单调递减,在
上单调递减,在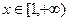 上单调递增.
上单调递增.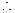 当
当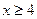 时,
时,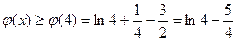 .
.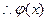 的最小值为
的最小值为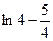 . ….4分
. ….4分
(Ⅱ)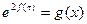 在
在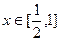 上有解
上有解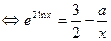 在
在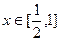 上有解
上有解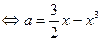 在
在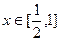 上有解.令
上有解.令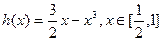 ,
,
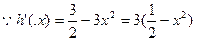 ,
,
令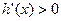 ,又
,又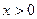 ,解得:
,解得: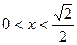 .
.
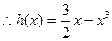 在
在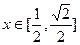 上单调递增,
上单调递增,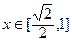 上单调递减,
上单调递减,
又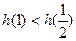 .
.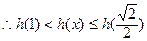 .即
.即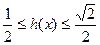 .故
.故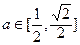 .……9分
.……9分
(Ⅲ)设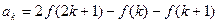 ,
,
由(I),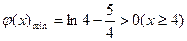 ,
,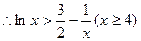 .
.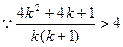 .
.

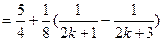 .
.
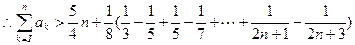
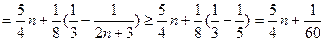 .
.
构造函数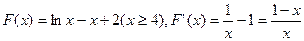 ,
,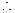 当
当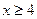 时,
时,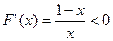 .
.
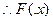 在
在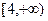 上单调递减,即
上单调递减,即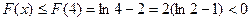 .
.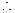 当
当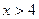 时,
时,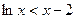 .
.
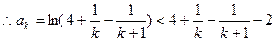 .即
.即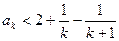 .
.
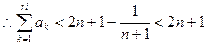 .
.
故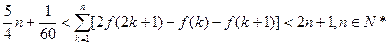 . …14分
. …14分
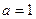 时,
时,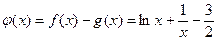 ,
,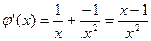 ,令
,令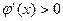 ,又
,又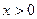 ,
,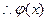 在
在 上单调递减,在
上单调递减,在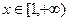 上单调递增.
上单调递增.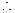 当
当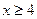 时,
时,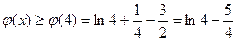 .
.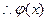 的最小值为
的最小值为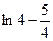 . ….4分
. ….4分(Ⅱ)
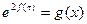 在
在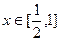 上有解
上有解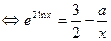 在
在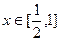 上有解
上有解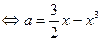 在
在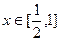 上有解.令
上有解.令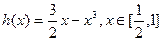 ,
,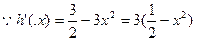 ,
,令
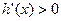 ,又
,又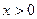 ,解得:
,解得: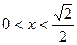 .
.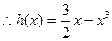 在
在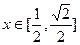 上单调递增,
上单调递增,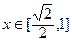 上单调递减,
上单调递减,又
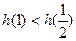 .
.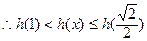 .即
.即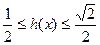 .故
.故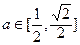 .……9分
.……9分(Ⅲ)设
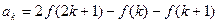 ,
,
由(I),
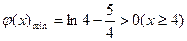 ,
,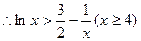 .
.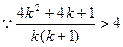 .
.
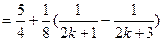 .
.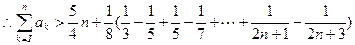
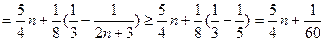 .
.构造函数
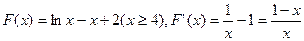 ,
,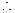 当
当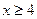 时,
时,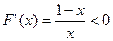 .
.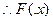 在
在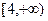 上单调递减,即
上单调递减,即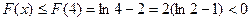 .
.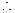 当
当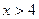 时,
时,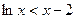 .
.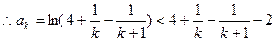 .即
.即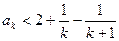 .
.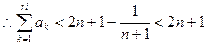 .
.故
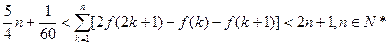 . …14分
. …14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
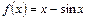 ,数列
,数列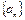 满足:
满足: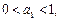
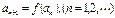 ,证明:
,证明:
 数
数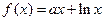
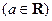 .
.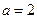 ,求曲线
,求曲线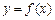 在
在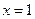 处切线的斜率;
处切线的斜率;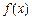 的单调区间;
的单调区间;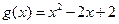 ,若对任意
,若对任意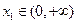 ,均存在
,均存在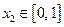 ,使得
,使得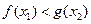 ,求
,求 的取值范围。
的取值范围。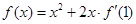 ,则
,则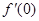 等于( )
等于( )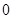
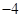
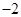
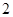
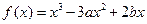 在点
在点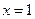 处有极小值
处有极小值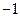 ,试确定
,试确定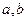 的值,并求出
的值,并求出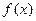 的单调区间。
的单调区间。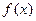 在定义域内可导,
在定义域内可导,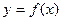 图象如下图所示,则导函数
图象如下图所示,则导函数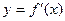 的图象可
的图象可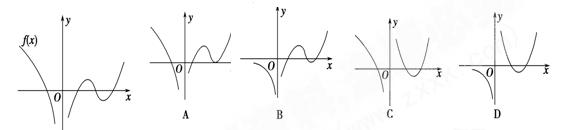
 近上点Q(1+Δx,3+Δy), 则
近上点Q(1+Δx,3+Δy), 则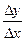 =( )
=( )