题目内容
在双曲线
=－1的一支上有不同的三点A(x1,y1),B(x2,6),C(x3,y3),与焦点F(0,5)的距离成等差数列.(1)求y1+y3的值;
(2)求证:线段AC的垂直平分线经过某一定点,并求出定点坐标.
(1)解:∵=e,∴|PF|=ey－a.
又A、B、C到F的距离成等差数列,
∴2(ey2－a)=(ey1－a)+(ey3－a).
∴y1+y3=2y2=12.
(2)证明:由题意,得
①－②,得
(y1－y3)(y1+y3)－
(x1－x3)(x1+x3)=0.
∴
.
若x1+x3=0,则kAC=0,y1=y3=y2=6,A、B、C三点共线,这是不可能的.
∴x1+x3≠0.则AC的中垂线方程为
y－6=－
(x－
),即y=－
.
因此,AC的中垂线过定点(0,
).
练习册系列答案
相关题目
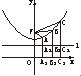如图，在双曲线
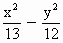＝－1的一支上有不同三点A
，6)，C(
)与焦点F(0，5)的距离成等差数列，(1)求
；(2)求证线段AC的垂直平分线经过某一定点，并求出定点的坐标．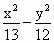
＝－1的一支上有不同的三点A(
，
)，B(
，6)，C(
，
)与焦点F(0，5)的距离成等差数列．
－
＝1的一支上有三个不同的点A(x1，y1)、B(
，6)、C(x2，y2)，它们与焦点F(0，5)的距离成等差数列，求y1＋y2的值．