题目内容
7.函数f(x)=$\frac{x}{\sqrt{1-{x}^{2}}}$的奇偶性为奇函数.分析 根据函数奇偶性的定义进行判断即可.
解答 解:由1-x2>0得-1<x<1,即函数的定义域为(-1,1)
∵f(-x)=$\frac{-x}{\sqrt{1-(-x)^{2}}}$=-$\frac{x}{\sqrt{1-{x}^{2}}}$=-f(x),
∴f(x)为奇函数,
故答案为:奇函数
点评 本题主要考查函数奇偶性的判断,根据函数的奇偶性的定义是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
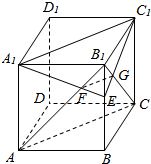 如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.
如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.