题目内容
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,且 .
.
(Ⅰ)求B的大小;
(Ⅱ)若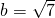 ,且△ABC的面积为
,且△ABC的面积为 ,求a+c的值.
,求a+c的值.
解:(Ⅰ)由 a=2bsinA,根据正弦定理得
a=2bsinA,根据正弦定理得 ,…(3分)
,…(3分)
所以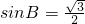 ,…(5分)
,…(5分)
由△ABC为锐角三角形得 . …(6分)
. …(6分)
(Ⅱ)由 ,且
,且 ,可得ac=6.…(8分)
,可得ac=6.…(8分)
根据余弦定理得,b2=a2+c2-2accosB,
∴a2+c2-ac=7.…(9分)
即(a+c)2=3ac+7=3×6+7=25.…(11分)
所以,a+c=5. …(12分)
分析:(Ⅰ)由 a=2bsinA,根据正弦定理求得
a=2bsinA,根据正弦定理求得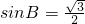 ,由此求得锐角B的值.
,由此求得锐角B的值.
(Ⅱ)由三角形的面积求得ac=6,由余弦定理求出a2+c2-ac=7,由此求出a+c的值.
点评:本题主要考查正弦定理、余弦定理的应用,解三角形,根据三角函数的值求角,属于中档题.
 a=2bsinA,根据正弦定理得
a=2bsinA,根据正弦定理得 ,…(3分)
,…(3分)所以
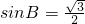 ,…(5分)
,…(5分)由△ABC为锐角三角形得
 . …(6分)
. …(6分)(Ⅱ)由
 ,且
,且 ,可得ac=6.…(8分)
,可得ac=6.…(8分)根据余弦定理得,b2=a2+c2-2accosB,
∴a2+c2-ac=7.…(9分)
即(a+c)2=3ac+7=3×6+7=25.…(11分)
所以,a+c=5. …(12分)
分析:(Ⅰ)由
 a=2bsinA,根据正弦定理求得
a=2bsinA,根据正弦定理求得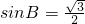 ,由此求得锐角B的值.
,由此求得锐角B的值.(Ⅱ)由三角形的面积求得ac=6,由余弦定理求出a2+c2-ac=7,由此求出a+c的值.
点评:本题主要考查正弦定理、余弦定理的应用,解三角形,根据三角函数的值求角,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目