题目内容
【题目】如图，在正四棱锥P﹣ABCD中，AB=2，PA= 
，E是棱PC的中点，过AE作平面分别与棱PB、PD交于M、N两点． 
（1）若PM= 
PB，PN=λPD，求λ的值；
（2）求直线PA与平面AMEN所成角的正弦值的取值范围．
【答案】
（1）解：连接AC、BD交于点O，以O为坐标原点建立如图所示的空间直角坐标系，则A（0，﹣ 
，0），B （ ，0，0），C（0， ，0），D（﹣ ，0，0），P（0，0，2），E（0， 
，1）
， 
， 
， 
， 
．
，
∵AN，AE，AM共面，∴ 
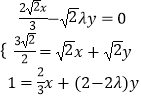
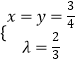
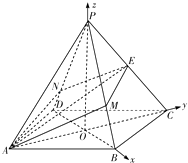
（2）解：根据正四棱锥P﹣ABCD的对称性可知，当PM=PN时，P到面AMEN的距离最大，此时直线PA与平面AMEN所角最大，
，P到面AMEN的距离最小，此时直线PA与平面AMEN所角最小．
①由（Ⅰ）知当PM=PN时，λ= 
， 
，
设面AMEN的法向量为 
，
由 
， 
取 
设直线PA与平面AMEN所成角为θ，sinθ=|cos＜ 
＞|= 
，
②当M在B时，因为AB∥面PDC，所以过AB，AE的面与面PDC的交线NE∥AB
设 
是面ABEN的法向量，
由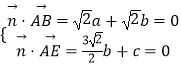 
，可取 
sinθ=|cos＜ 
＞|= 
．
直线PA与平面AMEN所成角的正弦值的取值范围为[ ， ]
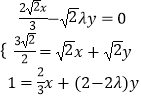
【解析】（1）连接AC、BD交于点O，以O为坐标原点建立如图所示的空间直角坐标系，则A（0，﹣ ，0），B （ ，0，0），C（0， ，0），D（﹣ ，0，0），P（0，0，2），E（0， ，1）由AN，AE，AM共面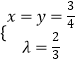， ．（2）根据正四棱锥P﹣ABCD的对称性可知，当PM=PN时，P到面AMEN的距离最大，此时直线PA与平面AMEN所角最大，P到面AMEN的距离最小，此时直线PA与平面AMEN所角最小．利用向量分别求出求解直线PA与平面AMEN所成角的正弦值．
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则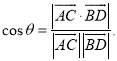
才能正确解答此题．
