题目内容
12.设抛物线C:y2=16x的焦点为F,点M在抛物线C上,若以MF为直径的圆过点A(0,2),则|MF|=5.分析 设M$(\frac{{y}^{2}}{16},y)$,根据以MF为直径的圆过点A(0,2),可得$\overrightarrow{AM}•\overrightarrow{AF}$=0,解得y即可得出.
解答 解:F(4,0),
设M$(\frac{{y}^{2}}{16},y)$,∵以MF为直径的圆过点A(0,2),
∴AM⊥AF,
∴$\overrightarrow{AM}•\overrightarrow{AF}$=$(\frac{{y}^{2}}{16},y-2)$•(4,-2)=0,
∴$\frac{{y}^{2}}{4}-2(y-2)$=0,
解得y=4,
∴xM=$\frac{{4}^{2}}{16}$=1,
∴|MF|=1+4=5.
故答案为:5.
点评 本题考查了圆的性质、抛物线的定义及其性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知三棱锥P-ABC的四个顶点均在同一球面上,其中△ABC为等边三角形,PA⊥平面ABC,PA=2AB=2a,则该球的体积是( )
| A. | $\frac{\sqrt{2}}{27}$πa2 | B. | $\frac{32\sqrt{2}}{27}$πa2 | C. | $\frac{32\sqrt{3}}{27}$πa3 | D. | $\frac{32\sqrt{3}}{9}$πa3 |
1.已知集合A={x|$\frac{1}{x}$<1},B={y|y=2-x-1,x∈R},则A∩B=( )
| A. | ∅ | B. | {x|x>1} | C. | {x|-1<x<0} | D. | {x|-1<x<0或x>1} |
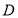 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数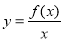 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间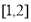 上不是“弱增”函数的为( )
上不是“弱增”函数的为( ) B.
B. C.
C. D.
D.
 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.