题目内容
若两曲线y=x2与y=cx3(c>0)围成图形的面积是 ,则c的值为
,则c的值为
- A.2
- B.

- C.3
- D.

B
分析:先求出两图象的交点坐标,进而利用定积分即可计算出答案.
解答:令x2=cx3(c>0),解得x=0或 ,
,
于是两曲线y=x2与y=cx3(c>0)围成图形的面积= =
= =
= .
.
∴ ,
,
∴ ,解得
,解得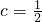 .
.
故选B.
点评:把阴影部分的面积转化为利用定积分求是解题的关键.
分析:先求出两图象的交点坐标,进而利用定积分即可计算出答案.
解答:令x2=cx3(c>0),解得x=0或
 ,
,于是两曲线y=x2与y=cx3(c>0)围成图形的面积=
 =
= =
= .
.∴
 ,
,∴
 ,解得
,解得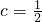 .
.故选B.
点评:把阴影部分的面积转化为利用定积分求是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ,则c的值为( )
,则c的值为( )

 ,则c的值为( )
,则c的值为( )
