Question

公差不为零的等差数列{a_n}中，a₃=7，又a₂，a₄，a₉成等比数列．
（1）求数列{a_n}的通项公式．
（2）设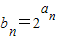，求数列{b_n}的前n项和S_n．

Answer 1

【答案】分析：（1）设数列的公差为d，根据a₃=7，又a₂，a₄，a₉成等比数列，可得（7+d）²=（7-d）（7+6d），从而可得d=3，进而可求数列{a_n}的通项公式；
（2）先确定数列{b_n}是等比数列，进而可求数列{b_n}的前n项和S_n．
解答：解：（1）设数列的公差为d，则
∵a₃=7，又a₂，a₄，a₉成等比数列．
∴（7+d）²=（7-d）（7+6d）
∴d²=3d
∵d≠0
∴d=3
∴a_n=7+（n-3）×3=3n-2
即a_n=3n-2；
（2）∵，∴
∴
∴数列{b_n}是等比数列，
∵
∴数列{b_n}的前n项和S_n=．
点评：本题考查等差数列与等比数列的综合，考查等差数列的通项，等比数列的求和公式，属于中档题．