Question

如图，在四棱锥S—ABCD中，底面ABCD，底面ABCD是矩形，且，E是SA的中点。

   （1）求证：平面BED平面SAB；

   （2）求平面BED与平面SBC所成二面角（锐角）的大小。

Answer 1

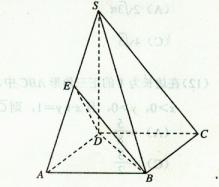
解：

（Ⅰ）∵SD⊥平面ABCD，∴平面SAD⊥平面ABCD，

∵AB⊥AD，∴AB⊥平面SAD，∴DE⊥AB．

∵SD＝AD，E是SA的中点，∴DE⊥SA，

∵AB∩SA＝A，∴DE⊥平面SAB

∴平面BED⊥平面SAB．                                                                       …4分

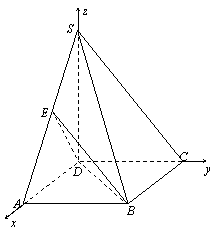
（Ⅱ）建立如图所示的坐标系D—xyz，不妨设AD＝2，则

D(0，0，0)，A(2，0，0)，B(2，，0)，

C(0，，0)，S(0，0，2)，E(1，0，1)．

＝(2，，0)，＝(1，0，1)，＝(2，0，0)，＝(0，－，2)．

设m＝(x₁，y₁，z₁)是面BED的一个法向量，则

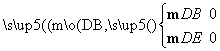即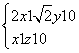

因此可取m＝(－1，，1)．                                                               …8分

设n＝(x₂，y₂，z₂)是面SBC的一个法向量，则

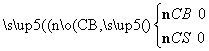即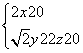

因此可取n＝(0，，1)．                                                            …10分

cosám，nñ＝＝＝，

故平面BED与平面SBC所成锐二面角的大小为30°．                        …12分