题目内容
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,焦点
,焦点![]() .
.
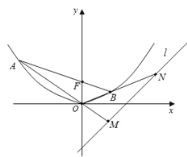
(1)求抛物线![]() 的方程;
的方程;
(2)过![]() 作直线交抛物线于
作直线交抛物线于![]() 、
、![]() 两点.若直线
两点.若直线![]() 、
、![]() 分别交直线
分别交直线![]() :
:![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由抛物线的几何性质及题设条件焦点![]() ,可直接求得
,可直接求得![]() ,确定出抛物线的开口方向,写出物线
,确定出抛物线的开口方向,写出物线![]() 的标准方程.
的标准方程.
(2)由题意,可![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,将直线方程与抛物线方程联立,写出韦达定理,再结合弦长公式求出
,将直线方程与抛物线方程联立,写出韦达定理,再结合弦长公式求出![]() ,分别求出
,分别求出![]() 和
和![]() 即可表示出
即可表示出![]() ,最后利用换元法和二次函数,即可求得
,最后利用换元法和二次函数,即可求得![]() 最小值.
最小值.
()由题意可设抛物线![]() 的方程为
的方程为![]() ,则
,则![]() ,解得
,解得![]() ,
,
故抛物线![]() 的方程为
的方程为![]() ;
;
(2)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,
,
从而有![]() ,
,
由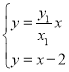 解得点
解得点![]() 的横坐标为
的横坐标为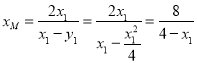 ,
,
同理可得点![]() 的横坐标为
的横坐标为![]() ,
,
所以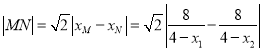
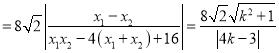 ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,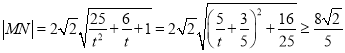 ,
,
综上所述,当![]() ,即
,即![]() 时,
时,![]() 的最小值是
的最小值是![]() .
.

练习册系列答案
相关题目
【题目】等差数列![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是下表第一、二、三行中的某一个数,且其中的任何两个数不在下表的同一列.
分别是下表第一、二、三行中的某一个数,且其中的任何两个数不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | 5 | 8 | 2 |
第二行 | 4 | 3 | 12 |
第三行 | 16 | 6 | 9 |
(1)请选择一个可能的![]() 组合,并求数列
组合,并求数列![]() 的通项公式;
的通项公式;
(2)记(1)中您选择的![]() 的前
的前![]() 项和为
项和为![]() ,判断是否存在正整数
,判断是否存在正整数![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列,若有,请求出
成等比数列,若有,请求出![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.