Question

3．若函数f（x）=x|x-a|-$\frac{a}{2}$恰有三个零点，则实数a的取值范围是（-∞，-2）∪（2，+∞）．

Answer 1

分析 讨论a=0，a＞0，a＜0，结合f（0）的符号，由函数的单调性和二次方程的判别式大于0，解不等式即可得到所求范围．

解答 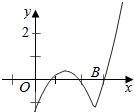解：当a=0时，f（x）=x|x|，只有一个零点0；
当a＞0时，f（0）=-$\frac{a}{2}$＜0，
当x＞a时，f（x）=x²-ax-$\frac{a}{2}$，对称轴x=$\frac{a}{2}$＜a，即有f（x）在（a，+∞）递增，
要有3个零点，必须0＜x＜a时，f（x）与x轴有两个交点，x＞a时有一个交点．
则0＜x＜a时，f（x）=ax-x²-$\frac{a}{2}$，判别式a²-2a＞0，解得a＞2；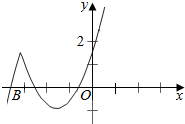
当a＜0时，f（0）=-$\frac{a}{2}$＞0，
当x＜a时，f（x）=-x²+ax-$\frac{a}{2}$，对称轴x=$\frac{a}{2}$＞a，即有f（x）在（-∞，a）递增
要有3个零点，必须a＜x＜0时，f（x）与x轴有两个交点，
x＜a时有一个交点．
则a＜x＜0时，f（x）=ax+x²-$\frac{a}{2}$，判别式a²+2a＞0，解得a＜-2．
综上可得a＞2或a＜-2．
故答案为：（-∞，-2）∪（2，+∞）．

点评 本题考查函数的零点的判断，考查分类讨论和数形结合的思想方法，注意运用单调性和二次方程的判别式，考查运算求解能力，属于中档题．