题目内容
在△ABC中,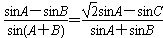 。
。
(1)求角B;
(2)若sinA=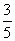 ,求cosC的值。
,求cosC的值。
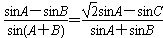 。
。(1)求角B;
(2)若sinA=
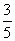 ,求cosC的值。
,求cosC的值。解:(1)依题意得
sin2A-sin2B=sin(A+B)(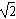 sinA-sinC) =
sinA-sinC) =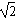 sinAsinC-sin2C,
sinAsinC-sin2C,
由正弦定理得:a2-b2=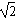 ac-c2,
ac-c2,
∴a2+c2-b2=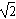 ac,
ac,
由余弦定理知:cosB=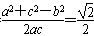 ,
,
∴B=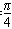 。
。
(2)∵sinA=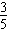 ,∴
,∴ <sinA<
<sinA<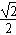 ,
,
∴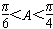 或
或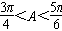 ,
,
又B=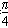 ,
,
∴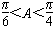 ,
,
∴cosA= ,
,
∴cosC=cos(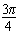 -A)=cos
-A)=cos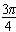 cosA+sin
cosA+sin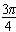 sinA=-
sinA=-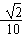 。
。
sin2A-sin2B=sin(A+B)(
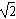 sinA-sinC) =
sinA-sinC) =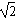 sinAsinC-sin2C,
sinAsinC-sin2C,由正弦定理得:a2-b2=
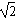 ac-c2,
ac-c2,∴a2+c2-b2=
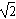 ac,
ac,由余弦定理知:cosB=
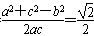 ,
,∴B=
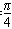 。
。(2)∵sinA=
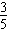 ,∴
,∴ <sinA<
<sinA<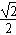 ,
, ∴
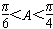 或
或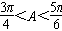 ,
,又B=
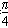 ,
,∴
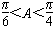 ,
,∴cosA=
 ,
, ∴cosC=cos(
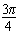 -A)=cos
-A)=cos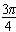 cosA+sin
cosA+sin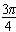 sinA=-
sinA=-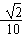 。
。
练习册系列答案
相关题目
在△ABC中,若b=1,c=
,∠C=
,则a=( )
| 3 |
| 2π |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
在△ABC中,若AB=1,BC=2,则角C的取值范围是( )
A、0<C≤
| ||||
B、0<C<
| ||||
C、
| ||||
D、
|