题目内容
(本小题满分12分)已知命题 :抛物线
:抛物线 与直线
与直线 有两个不同交点;命题
有两个不同交点;命题 :函数
:函数 在
在 上单调递增;若
上单调递增;若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数 的取值范围。
的取值范围。
 或
或
【解析】
试题分析:命题 :抛物线
:抛物线 与直线
与直线 有两个不同交点;把
有两个不同交点;把 代入
代入 中得:
中得:
 ,所以
,所以 ,推出
,推出  ;命题
;命题 :
: 恒成立,所以
恒成立,所以 , 解得:
, 解得: ,由
,由 或
或 为真,
为真, 且
且 为假,所以p与q为一真一假,
为假,所以p与q为一真一假,
按要求求出 的取值范围即可;
的取值范围即可;
试题解析:命题 :抛物线
:抛物线 与直线
与直线 有两个不同交点;把
有两个不同交点;把 代入
代入 中得:方程
中得:方程 有两个不相等的实根,命题
有两个不相等的实根,命题 :
: 恒成立,所以
恒成立,所以 , ∴
, ∴  ;因为p或q为真,p且q为假,所以p与q为一真一假,
;因为p或q为真,p且q为假,所以p与q为一真一假,
(1)当 为真
为真 为假时,
为假时,
(2)当 为假
为假 为真时,
为真时,
综上所述得:m的取值范围是 或
或
考点:复合命题的真假;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,则
,则
 (B)
(B)
 (D)
(D)

 B.
B. C.
C. D.
D.
 ,若
,若 的图像如图所示:
的图像如图所示:
 的图像是
的图像是
 则满足
则满足 的非空集合
的非空集合 的个数是
的个数是 成等比数列,且不等式
成等比数列,且不等式 的解集为
的解集为 ,则
,则 = 。
= 。  ,则目标函数
,则目标函数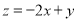 的最大值是( )
的最大值是( )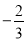
 发出的光线,沿平行于抛物线
发出的光线,沿平行于抛物线 的对称轴方向射向此抛物线上的点
的对称轴方向射向此抛物线上的点 ,经抛物线反射后,穿过焦点射向抛物线上的点
,经抛物线反射后,穿过焦点射向抛物线上的点 ,再经抛物线反射后射向直线
,再经抛物线反射后射向直线 上的点
上的点 ,经直线反射后又回到点
,经直线反射后又回到点 ,则
,则 等于( )
等于( )
 B.
B. C.
C. D.
D.
 中,
中,  ,则
,则 = .
= .