题目内容
 如图,ABCD是一块边长为2a的正方形铁板,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱,若水箱的高度x与底面边长的比不超过常数k(k>0).
如图,ABCD是一块边长为2a的正方形铁板,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱,若水箱的高度x与底面边长的比不超过常数k(k>0).(1)写出水箱的容积V与水箱高度x的函数表达式,并求其定义域;
(2)当水箱高度x为何值时,水箱的容积V最大,并求出其最大值.
分析:(1)由图形据体积公式得出体积关于高x的函数,再由题意中的限制条件得出定义域.
(2)宜用导数法求最值,先求导,解相关的不等式,列表,得出单调性求出最值.
(2)宜用导数法求最值,先求导,解相关的不等式,列表,得出单调性求出最值.
解答:解:(Ⅰ)由水箱的底面边长为2a-2x,高为x,得V=(2a-2x)2•x=4x•(a-x)2,
∵
∴
又a-
=
>0,0<x≤
,
∴故定义域为{x|0<x≤
}.(5分)
(Ⅱ)∵V=4x•(a-x)2=4x3-8ax2+4a2x,
∴V′=12x2-16ax+4a2,
令V′=0,得x=
,或x=a(舍)
若
≤
,即k≥
时,

∴当x=
时,V取得最大值,且最大值为
a3.
若
>
,即0<k<
时,V′(x)=12x2-16ax+4a2>0,
∴V在(0,
]上是增函数,
∴当x=
时,V取得最大值,且最大值为
a3.
综上可知,当k≥
时,x=
,水箱容积V取最大值
a3;
当0<k<
时,x=
,水箱容积V取最大值
a3.(13分)
∵
|
|
又a-
| 2ak |
| 1+2k |
| a |
| 1+2k |
| 2ak |
| 1+2k |
∴故定义域为{x|0<x≤
| 2ak |
| 1+2k |
(Ⅱ)∵V=4x•(a-x)2=4x3-8ax2+4a2x,
∴V′=12x2-16ax+4a2,
令V′=0,得x=
| a |
| 3 |
若
| a |
| 3 |
| 2ak |
| 1+2k |
| 1 |
| 4 |

∴当x=
| a |
| 3 |
| 16 |
| 27 |
若
| a |
| 3 |
| 2ak |
| 1+2k |
| 1 |
| 4 |
∴V在(0,
| 2ak |
| 1+2k |
∴当x=
| 2ak |
| 1+2k |
| 8k |
| (1+2k3) |
综上可知,当k≥
| 1 |
| 4 |
| a |
| 3 |
| 16 |
| 27 |
当0<k<
| 1 |
| 4 |
| 2ak |
| 1+2k |
| 8k |
| (1+2k3) |
点评:考查长方体的体积公式以及用导数数求最值的过程.题型比较基本,运算量不小.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
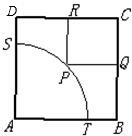 如图,ABCD是一块边长为100m的正方形地皮,其中AST是半径为90m的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形的停车场,使矩形的一个顶点P在圆弧ST上,相邻两边CQ,CR落在正方形的BC,CD边上,求矩形停车场PQCR面积的最大值与最小值.
如图,ABCD是一块边长为100m的正方形地皮,其中AST是半径为90m的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形的停车场,使矩形的一个顶点P在圆弧ST上,相邻两边CQ,CR落在正方形的BC,CD边上,求矩形停车场PQCR面积的最大值与最小值.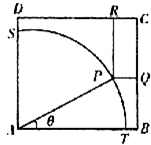 随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR.
随着机动车数量的增加,对停车场所的需求越来越大,如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一座半径为90米的扇形小山,P是弧TS上一点,其余部分都是平地,现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR. 如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为80米的扇形小山,P是弧TS上一点,其余部分都是平地.现一开发商想在平地上建造一个有边落在BC与CD上的长方形停车场PQCR.设∠PAT为θ,长方形停车场面积为S.
如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为80米的扇形小山,P是弧TS上一点,其余部分都是平地.现一开发商想在平地上建造一个有边落在BC与CD上的长方形停车场PQCR.设∠PAT为θ,长方形停车场面积为S. (2004•黄埔区一模)如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为90米的底面为扇形小山(P为
(2004•黄埔区一模)如图,ABCD是一块边长为100米的正方形地皮,其中ATPS是一半径为90米的底面为扇形小山(P为
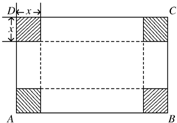 如图,ABCD是一块矩形铁板AB=48cm,BC=30cm,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱.
如图,ABCD是一块矩形铁板AB=48cm,BC=30cm,剪掉四个阴影部分的小正方形,沿虚线折叠后,焊接成一个无盖的长方体水箱.