题目内容
已知抛物线C:y2=4x的焦点为F,直线y=2x-4与C交于A,B两点,则cos∠AFB等于( )
A.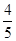 | B.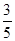 | C.-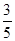 | D.-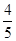 |
D
方法一:由 得
得 或
或
令B(1,-2),A(4,4),又F(1,0),
∴由两点间距离公式得|BF|=2,|AF|=5,|AB|=3 .
.
∴cos∠AFB= =
=
=-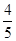 .
.
方法二:由方法一得A(4,4),B(1,-2),F(1,0),
∴ =(3,4),
=(3,4), =(0,-2),
=(0,-2),
∴| |=
|= =5,|
=5,| |=2.
|=2.
∴cos∠AFB= =
= =-
=-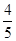 .
.
 得
得 或
或
令B(1,-2),A(4,4),又F(1,0),
∴由两点间距离公式得|BF|=2,|AF|=5,|AB|=3
 .
.∴cos∠AFB=
 =
=
=-
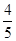 .
.方法二:由方法一得A(4,4),B(1,-2),F(1,0),
∴
 =(3,4),
=(3,4), =(0,-2),
=(0,-2),∴|
 |=
|= =5,|
=5,| |=2.
|=2.∴cos∠AFB=
 =
= =-
=-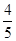 .
.
练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
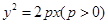 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且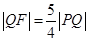 .
.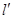 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.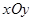 中,原点为
中,原点为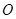 ,抛物线
,抛物线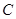 的方程为
的方程为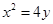 ,线段
,线段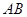 是抛物线
是抛物线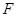 ;
;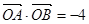 ,求证:直线
,求证:直线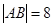 时,设圆
时,设圆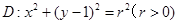 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦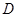 相切,求半径
相切,求半径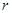 的取值范围?
的取值范围?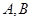 是抛物线
是抛物线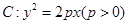 上不同的两点,点
上不同的两点,点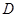 在抛物线
在抛物线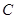 的准线
的准线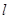 上,且焦点
上,且焦点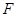 到直线
到直线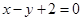 的距离为
的距离为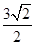 .
.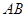 过焦点
过焦点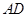 过原点
过原点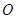 ;③直线
;③直线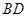 平行
平行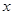 轴.
轴.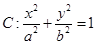
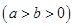 的右焦点
的右焦点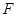
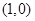 ,长轴的左、右端点分别为
,长轴的左、右端点分别为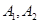 ,且
,且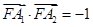 .
.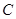 的方程;
的方程;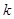 (
( )的直线
)的直线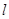 交椭圆
交椭圆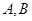 两点,弦
两点,弦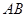 的垂直平分线与
的垂直平分线与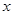 轴相交于
轴相交于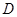 点. 试问椭圆
点. 试问椭圆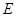 使得四边形
使得四边形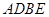 为菱形?若存在,求
为菱形?若存在,求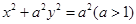 的一个顶点
的一个顶点 为直角顶点作此椭圆的内接等腰直角三角形
为直角顶点作此椭圆的内接等腰直角三角形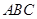 ,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?
,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?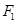 ,
,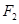 是双曲线
是双曲线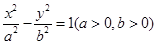 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点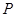 与点
与点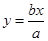 对称,则该双曲线的离心率为
对称,则该双曲线的离心率为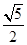
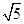
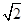
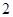
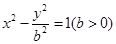 的一条渐近线与圆
的一条渐近线与圆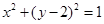 至多有一个交点,则双曲线离心
至多有一个交点,则双曲线离心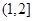
 的中心在原点,焦点在
的中心在原点,焦点在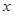 轴上,椭圆上的点到焦点的最小距离为
轴上,椭圆上的点到焦点的最小距离为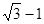 ,离心率
,离心率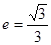 .
.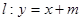 交
交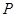 、
、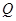 两点,点
两点,点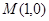 ,问是否存在
,问是否存在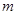 ,使
,使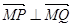 ?若存在求出
?若存在求出