Question

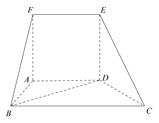
【题目】如图，在多面体中，平面平面，四边形为正方形，四边形为梯形，且，，．

（1）求证：平面；

（2）在线段上是否存在点，使得平面？若存在，求出的值；若不存在，请说明理由.

Answer 1

【答案】（1）证明见解析 （2）存在，.

【解析】

（1）由面面垂直的性质证明，再由已知求解三角形证明，由线面垂直的判定可得平面；
（2）取中点，连接，连接交于点，可证平面，此时得到．

（1）因为四边形为正方形，

所以.平面平面，

平面平面，

所以平面.所以.

取中点，连接.由，，，

可得四边形为正方形.

所以.所以.所以.

因为，所以平面.

（2）存在，当为的中点时，平面，此时.

证明如下：

取中点，连接，连接交于点，由于四边形为正方形，

所以是的中点，同时也是的中点.

因为，又四边形为正方形，

所以，

连接，所以四边形为平行四边形.

所以.又因为平面，平面，

所以平面.