题目内容
【题目】在实数集![]() 中,定义两个实数
中,定义两个实数![]() 、
、![]() 的运算法则△如下:若
的运算法则△如下:若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() .
.
(1)请分别计算![]() 和
和![]() 的值;
的值;
(2)对于实数![]() ,判断
,判断![]() 是否恒成立,并说明理由;
是否恒成立,并说明理由;
(3)求函数![]() 的解析式,其中
的解析式,其中![]() ,并求函数的最值.(符号“
,并求函数的最值.(符号“![]() ”表示相乘)
”表示相乘)
【答案】(1)9;9(2)不恒成立(3)最大值为2,最小值为-4.
【解析】
(1)根据题干条件,比较大小,代入关系式计算即可. (2)实数![]() ,但是
,但是![]() 大小关系不确定, 所以
大小关系不确定, 所以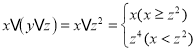 ,
,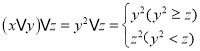 不能恒等. (3)根据
不能恒等. (3)根据![]() 与1的大小关系对
与1的大小关系对![]() 分类讨论,讨论每一段的最值再最终求最值即可.
分类讨论,讨论每一段的最值再最终求最值即可.
解:(1)![]() ,
,![]() .
.
(2)![]()
![]() ,
,![]() 不一定小于
不一定小于![]() ,所以
,所以![]()
![]() ;
;
![]() ,
,![]() ,
,![]() 不一定小于
不一定小于![]() ,所以
,所以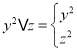
![]() ;
;
所以![]() 不恒成立.
不恒成立.
(3)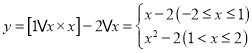 ,
,
当![]() 时,
时,![]() 在
在![]() 处取得最大值-1,在
处取得最大值-1,在![]() 取得最小值-4,;
取得最小值-4,;
当![]() 时,
时,![]() 在
在![]() 处取得最大值2,在
处取得最大值2,在![]() 处取得最小值-1,
处取得最小值-1,
所以![]() 的最大值为2,最小值为-4.
的最大值为2,最小值为-4.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目