题目内容
(本小题满分12分)
在锐角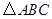 中,内角
中,内角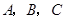 对边的边长分别是
对边的边长分别是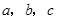 ,且
,且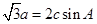
(1)求角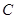 的值;
的值;
(2)若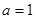 ,
,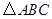 的面积为
的面积为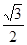
 ,求
,求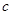 的值。
的值。
(1), 。(Ⅱ)
。(Ⅱ) 。
。
解析试题分析:(Ⅰ)由 a=2csinA及正弦定理得,
a=2csinA及正弦定理得, sinA=2sinCsinA,得sinC=
sinA=2sinCsinA,得sinC=  ,从而得到C值.
,从而得到C值.
(Ⅱ)由面积公式得S=  absinC=
absinC=  ×3×bsin
×3×bsin  =
=  ,解方程求得边长b.
,解方程求得边长b.
解:(1)由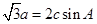 及正弦定理得,
及正弦定理得, ,…………………….4分
,…………………….4分
 ,
, 是锐角三角形,
是锐角三角形, 。 ………6分
。 ………6分
(Ⅱ)由面积公式得, ,
, ,
, , ……….9分
, ……….9分
由余弦定理得,
 ,,
,, 。……….12分考点:本题主要考查利用正弦定理解三角形,三角形面积公式的应用,
。……….12分考点:本题主要考查利用正弦定理解三角形,三角形面积公式的应用,
点评:解决该试题的关键是由 a=2csinA及正弦定理得,
a=2csinA及正弦定理得, sinA=2sinCsinA,并由此得到角C的正弦值。
sinA=2sinCsinA,并由此得到角C的正弦值。

练习册系列答案
相关题目
 ,
, ,
,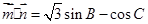 .
.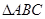 中,角
中,角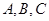 所对的边分别为
所对的边分别为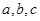 ,且满足
,且满足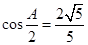 ,
,
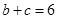 ,求
,求 的值.
的值. 中内角
中内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 .
. ,
, 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为 ,求
,求 的取值范围.
的取值范围. 的三边长分别为
的三边长分别为 已知
已知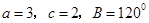 .
. 的长;(2) 求
的长;(2) 求 的面积
的面积
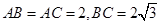 ,点D 在BC边上,∠ADC=45°。
,点D 在BC边上,∠ADC=45°。 的大小;(2)求AD的长。
的大小;(2)求AD的长。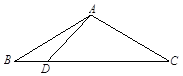
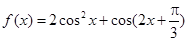
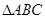 中,
中,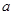 ,
,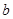 ,
, 分别是角
分别是角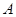 ,
,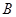 ,
,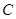 的对边;若
的对边;若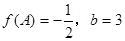 , sin(A
, sin(A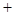 C)=
C)=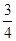 sinC,求
sinC,求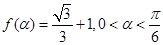 ,求
,求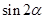 的值;
的值;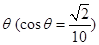 方向300 km的海面P处,并以20 km / h的速度向西偏北
方向300 km的海面P处,并以20 km / h的速度向西偏北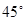 的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?