题目内容
函数f(x)=In(| x+1 |
分析：欲求原函数的反函数，即从原函数式f(x)=In(
-1)(x＞0)中反解出x，后再进行x，y互换，即得反函数的解析式．
| x+1 |
解答：解：∵f(x)=In(
-1)(x＞0)，
∴x=e2y+2ey，
∴x，y互换，得y=e2x+2ex（x∈R）．
故填：e2x+2ex（x∈R）．
| x+1 |
∴x=e2y+2ey，
∴x，y互换，得y=e2x+2ex（x∈R）．
故填：e2x+2ex（x∈R）．
点评：本题考查反函数的求法，要会求一些简单函数的反函数，掌握互为反函数的函数图象间的关系．
练习册系列答案
阅读快车系列答案
相关题目
+
(
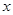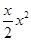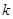≥0)。
+
(
≥0)。
+
(
≥0)。