题目内容
已知椭圆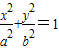 的两焦点分别为F1、F2,点P是以F1F2为直径的圆与椭圆的交点,若∠PF1F2=5∠PF2F1,则椭圆离心率为( )
的两焦点分别为F1、F2,点P是以F1F2为直径的圆与椭圆的交点,若∠PF1F2=5∠PF2F1,则椭圆离心率为( )A.
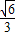
B.
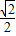
C.
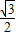
D.
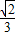
【答案】分析:根据题意可知∠F1PF2=90°,∠PF1F2=5∠PF2F1,进而求得∠PF1F2和∠PF2F1,在Rt△PF1F2分别表示出|PF1|和|PF2|,根据椭圆的定义可得2a=|PF1|+|PF2|,进而求得a和c的关系,从而求出椭圆的离心率.
解答:解:∵点P是以F1F2为直径的圆与椭圆的交点,
∴∠F1PF2=90°
∵∠PF1F2=5∠PF2F1,
∴∠PF1F2=15°,∠PF2F1=75°
在直角三角形F1PF2中,|PF1|=|F1F2|sin∠PF2F1=2c•sin75°,|PF2|=|F1F2|sin∠PF1F2=2c•sin15°,
∵2a=|PF1|+|PF2|
∴2a=2c•sin75°+2c•sin15°=4csin45°cos30°=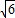 c
c
∴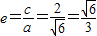
故选A.
点评:本题以椭圆为载体,考查椭圆的几何性质,求椭圆的离心率的关键是找出a和c的关系.
解答:解:∵点P是以F1F2为直径的圆与椭圆的交点,
∴∠F1PF2=90°
∵∠PF1F2=5∠PF2F1,
∴∠PF1F2=15°,∠PF2F1=75°
在直角三角形F1PF2中,|PF1|=|F1F2|sin∠PF2F1=2c•sin75°,|PF2|=|F1F2|sin∠PF1F2=2c•sin15°,
∵2a=|PF1|+|PF2|
∴2a=2c•sin75°+2c•sin15°=4csin45°cos30°=
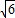 c
c∴
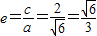
故选A.
点评:本题以椭圆为载体,考查椭圆的几何性质,求椭圆的离心率的关键是找出a和c的关系.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 的两焦点分别为
的两焦点分别为 ,且椭圆上的点到
,且椭圆上的点到 的最小距离为
的最小距离为 .
. 作直线
作直线 交椭圆
交椭圆 两点,设线段
两点,设线段 的中垂线交
的中垂线交 轴于
轴于 ,求m的取值范围.
,求m的取值范围.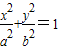 的两焦点分别为F1、F2,点P是以F1F2为直径的圆与椭圆的交点,若∠PF1F2=5∠PF2F1,则椭圆离心率为( )
的两焦点分别为F1、F2,点P是以F1F2为直径的圆与椭圆的交点,若∠PF1F2=5∠PF2F1,则椭圆离心率为( )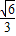
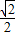
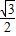
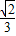
 的两焦点分别为F1,F2,P是椭圆在第一象限内的一点,并满足
的两焦点分别为F1,F2,P是椭圆在第一象限内的一点,并满足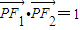 ,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.
,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.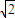 )时,求直线AB的方程;
)时,求直线AB的方程;