题目内容
(本小题共l2分)
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
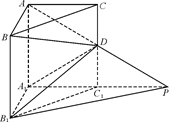
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;

本小题主要考查直三棱柱的性质、线面关系、二面角等基本知识,并考查空间想象能力和逻辑推理能力,考查应用向量知识解决问题的能力.


解法一:
(Ⅰ)连结AB1与BA1交于点O,连结OD,
∵C1D∥平面AA1,A1C1∥AP,∴AD=PD,又AO=B1O,
∴OD∥PB1,又ODÌ面BDA1,PB1Ë面BDA1,
∴PB1∥平面BDA1.
(Ⅱ)过A作AE⊥DA1于点E,连结BE.∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,
∴BA⊥平面AA1C1C.由三垂线定理可知BE⊥DA1.
∴∠BEA为二面角A-A1D-B的平面角.
在Rt△A1C1D中, ,
,
又 ,∴
,∴ .
.
在Rt△BAE中, ,∴
,∴ .
.
故二面角A-A1D-B的平面角的余弦值为 .
.
解法二:
如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A1-B1C1A,则 ,
, ,
, ,
, ,
, .
.
(Ⅰ)在△PAA1中有 ,即
,即 .
.
∴ ,
, ,
, .
.
设平面BA1D的一个法向量为 ,
,
则 令
令 ,则
,则 .
.
∵ ,
,
∴PB1∥平面BA1D,
(Ⅱ)由(Ⅰ)知,平面BA1D的一个法向量 .
.
又 为平面AA1D的一个法向量.∴
为平面AA1D的一个法向量.∴ .
.
故二面角A-A1D-B的平面角的余弦值为 .
.


解法一:
(Ⅰ)连结AB1与BA1交于点O,连结OD,
∵C1D∥平面AA1,A1C1∥AP,∴AD=PD,又AO=B1O,
∴OD∥PB1,又ODÌ面BDA1,PB1Ë面BDA1,
∴PB1∥平面BDA1.
(Ⅱ)过A作AE⊥DA1于点E,连结BE.∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,
∴BA⊥平面AA1C1C.由三垂线定理可知BE⊥DA1.
∴∠BEA为二面角A-A1D-B的平面角.
在Rt△A1C1D中,
 ,
,又
 ,∴
,∴ .
.在Rt△BAE中,
 ,∴
,∴ .
.故二面角A-A1D-B的平面角的余弦值为
 .
.解法二:
如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A1-B1C1A,则
 ,
, ,
, ,
, ,
, .
.(Ⅰ)在△PAA1中有
 ,即
,即 .
.∴
 ,
, ,
, .
.设平面BA1D的一个法向量为
 ,
,则
 令
令 ,则
,则 .
.∵
 ,
,∴PB1∥平面BA1D,
(Ⅱ)由(Ⅰ)知,平面BA1D的一个法向量
 .
.又
 为平面AA1D的一个法向量.∴
为平面AA1D的一个法向量.∴ .
.故二面角A-A1D-B的平面角的余弦值为
 .
.略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
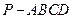 ,底面
,底面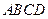 是边长为2的正方形,
是边长为2的正方形,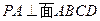 ,
,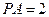 ,过点
,过点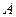 作
作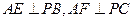 ,连接
,连接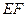 .
.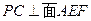 .
.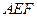 交侧棱
交侧棱 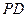 于点
于点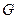 ,求多面体
,求多面体 的体积。
的体积。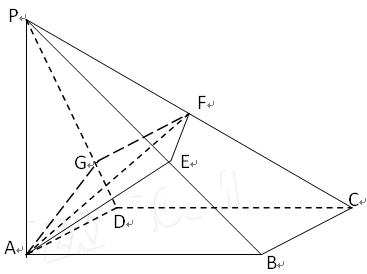
 平面
平面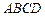 ,
,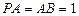 ,
,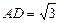 ,
,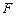 是
是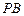 中点,点
中点,点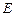 在
在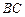 边上.
边上.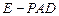 的体积;
的体积;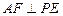 ;
;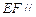 平面
平面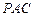 ,试确定
,试确定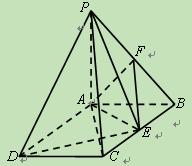
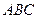 —
—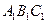 中,若∠BAC=
中,若∠BAC= ,
,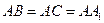 ,则异面直线
,则异面直线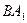 与
与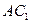 所成的角等于_________
所成的角等于_________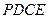 为矩形,四边形
为矩形,四边形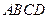 为梯形,平面
为梯形,平面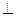 平面
平面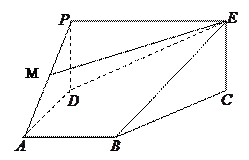
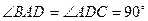 ,
,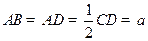 ,
, .
. (Ⅰ)若
(Ⅰ)若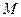 为
为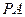 中点,求证:
中点,求证: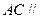 平面
平面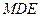 ;
;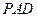 与
与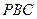 所成锐二面角的大小.
所成锐二面角的大小. 
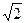 ,BC=CC1=1,P是BC1上一动点,则
,BC=CC1=1,P是BC1上一动点,则 的最小值是_____.
的最小值是_____.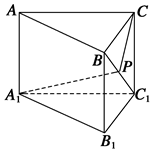
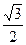


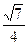
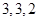 的三角形,则该圆锥的侧面积是 。
的三角形,则该圆锥的侧面积是 。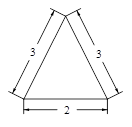
 体
体 的棱长为1,若以
的棱长为1,若以 的方向为左视方向,则该正四面体的左视图与俯视图面积和的取值范围为 .
的方向为左视方向,则该正四面体的左视图与俯视图面积和的取值范围为 .