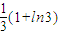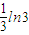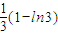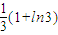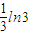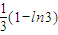题目内容
设动直线x=m与函数f（x）=x3，g（x）=lnx的图象分别交于点M、N，则|MN|的最小值为（ ）
A．
| B．
| C．
| D．ln3-1 |
画图可以看到|MN|就是两条曲线间的垂直距离．
设F（x）=f（x）-g（x）=x3-lnx，
求导得：F'（x）=3x2-
．
令F′（x）＞0得x＞
；令F′（x）＜0得0＜x＜
所以当x=
时，F（x）有最小值为F（
）=
(1+ln3)
故选A
设F（x）=f（x）-g（x）=x3-lnx，
求导得：F'（x）=3x2-
| 1 |
| x |
令F′（x）＞0得x＞
| ||
| 3 |
| ||
| 3 |
所以当x=
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
故选A
练习册系列答案
轻松暑假总复习系列答案
相关题目
设动直线x=m与函数f（x）=x3，g（x）=lnx的图象分别交于点M、N，则|MN|的最小值为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、ln3-1 |
