题目内容
已知函数![]() ,且其导函数
,且其导函数![]() 的图像过原点.
的图像过原点.
(1)当a=1时,求函数f(x)的图像在x=3处的切线方程;
(2)若存在x<0,使得![]() ,求a的最大值;
,求a的最大值;
(3)当a>0时,求函数f(x)的零点个数.
答案:
解析:
解析:
|
解: 由 (1)当 所以函数 (2)存在 当且仅当 (3)当
又 所以函数 故函数 注:①证明 设 则 当 函数 故函数 从而 ②证明函数 当 故函数 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

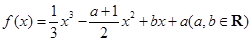 ,且其导函数
,且其导函数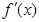 的图像过原点.
的图像过原点.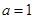 时,求函数
时,求函数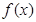 的图像在
的图像在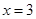 处的切线方程;
处的切线方程;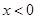 ,使得
,使得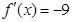 ,求
,求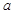 的最大值;
的最大值; 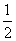 x2,g(x)=logax(a>0且a≠1),
x2,g(x)=logax(a>0且a≠1),