题目内容
已知f(x)=2x-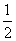 x2,g(x)=logax(a>0且a≠1),
x2,g(x)=logax(a>0且a≠1),
(Ⅰ)过P(0,2)作曲线y=f(x)的切线,求切线方程;
(Ⅱ)设h(x)=f(x)-g(x)在定义域上为减函数,且其导函数y=h′(x)存在零点,求实数a的值。
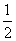 x2,g(x)=logax(a>0且a≠1),
x2,g(x)=logax(a>0且a≠1),(Ⅰ)过P(0,2)作曲线y=f(x)的切线,求切线方程;
(Ⅱ)设h(x)=f(x)-g(x)在定义域上为减函数,且其导函数y=h′(x)存在零点,求实数a的值。
解:(Ⅰ)f(0)=0,
∴P(0,2)不在曲线y=f(x)上,
设切点为Q(x0,y0),
∵f′(x)=2-x,
∴k=f′(x0)=2-x0,且y0=f(x0)= ,
,
∴切线 ,即
,即 ,
,
∵(0,2)在切线上,代入可得x0=±2,
∴切线为y=2或y=4x+2;
(Ⅱ)h(x) 在(0,+∞)递减,
在(0,+∞)递减,
∴h′(x)= 在x>0时恒成立,
在x>0时恒成立,
∵x>0,
∴ 在x>0恒成立,
在x>0恒成立,
x>0时,2x-x2∈(-∞,1],
∴ ,∴0<lna≤1,①
,∴0<lna≤1,①
又∵h′(x)= 存在零点,即方程lna·x2-21na·x+1=0有正根,
存在零点,即方程lna·x2-21na·x+1=0有正根,
∴Δ=4ln2a-4lna≥0,
∴lna≥1或lna<0,②
由①②知lna=1,
∴a=e。
∴P(0,2)不在曲线y=f(x)上,
设切点为Q(x0,y0),
∵f′(x)=2-x,
∴k=f′(x0)=2-x0,且y0=f(x0)=
 ,
,∴切线
 ,即
,即 ,
, ∵(0,2)在切线上,代入可得x0=±2,
∴切线为y=2或y=4x+2;
(Ⅱ)h(x)
 在(0,+∞)递减,
在(0,+∞)递减,∴h′(x)=
 在x>0时恒成立,
在x>0时恒成立,∵x>0,
∴
 在x>0恒成立,
在x>0恒成立,x>0时,2x-x2∈(-∞,1],
∴
 ,∴0<lna≤1,①
,∴0<lna≤1,① 又∵h′(x)=
 存在零点,即方程lna·x2-21na·x+1=0有正根,
存在零点,即方程lna·x2-21na·x+1=0有正根,∴Δ=4ln2a-4lna≥0,
∴lna≥1或lna<0,②
由①②知lna=1,
∴a=e。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目