题目内容

【题目】如图放置的边长为1的正方形沿轴顺时针滚动一周，设顶点的运动轨迹与轴所围区域为，若在平面区域内任意取一点，则所取的点恰好落在区域内部的概率为

A. B. C. D.

【答案】C

【解析】

顶点的运动轨迹，分三部分：前一部分的图象为四分之一圆周，后一部分的图象为四分之一圆周，且半径都是1,中间部分的轨迹为以为半径的四分之一圆周，分别求出与轴围成的面积，求和后利用几何概型概率公式求解即可.

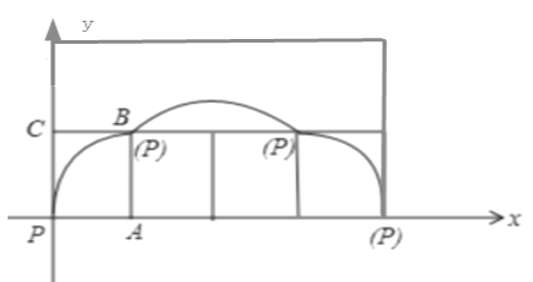
正方形沿轴顺时针滚动一周，顶点的运动轨迹，分三部分：前一部分的图象为四分之一圆周，后一部分的图象为四分之一圆周，且半径都是1,此时两部分扇形所占面积为,中间部分的轨迹为以为四分之一圆周，与围成的面积为,顶点的运动轨迹与轴所围区域的面积为，

平面区域的面积为，

所以在平面区域内任意取一点，

则所取的点恰好落在区域内部的概率为故选C.

练习册系列答案
相关题目

【题目】某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的年收益与投资额成正比，其关系如图1；投资股票等风险型产品的年收益与投资额的算术平方根成正比，其关系如图2.

（1）分别写出两种产品的年收益和的函数关系式；

（2）该家庭现有20万元资金，全部用于理财投资，问:怎么分配资金能使投资获得最大年收益，其最大年收益是多少万元?

【题目】下列说法中，正确的有_______.(写出所有正确说法的序号)

①在中，若，则；

②在中，若，则是锐角三角形；

③在中，若，则；

④若是等差数列，其前项和为，则三点共线；

⑤等比数列的前项和为，若对任意的，点均在函数(且，均为常数)的图象上，则的值为.

【题目】下面结论中，正确结论的是（ ）

A.存在两个不等实数，使得等式成立

B. (0< x < π)的最小值为4

C.若是等比数列的前项的和，则成等比数列

D.已知的三个内角所对的边分别为，若，则一定是锐角三角形

【题目】某商场经销某商品，根据以往资料统计，顾客采用的付款期数的分布列为

1

2

3

4

5

0.2

0.3

0.3

0.1

0.1

商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为300元；分4期或5期付款，其利润为400元，表示经销一件该商品的利润.

（1）求事件：“购买该商品的3位顾客中，至少有1位采用期付款”的概率；

（2）求的分布列、期望和方差.

【题目】在中，已知A，a，b，给出下列说法：

①若，则此三角形最多有一解；

②若，且，则此三角形为直角三角形，且；

③当，且时，此三角形有两解.

其中正确说法的个数为（ ）

A.0B.1C.2D.3

【题目】为改善居民的生活环境，政府拟将一公园进行改造扩建.已知原公园是直径为200 m的半圆形，出入口在圆心O处，A为居民小区，OA的距离为200 m，按照设计要求，以居民小区A和圆弧上点B的连线为一条边向半圆外作等腰直角三角形ABC（C为直角顶点），使改造后的公园如图中四边形OACB所示.

（1）若，则C与出入口O之间的距离为多少米？

（2）的大小为多少时，公园OACB的面积最大？

【题目】在平面直角坐标系中,已知直线的参数方程为（为参数）.在以坐标原点为极点,轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线的极坐标方程是.

（1）求直线的普通方程与曲线的直角坐标方程；

（2）设点.若直与曲线相交于两点,求的值.

【题目】已知，的线性回归直线方程为，且，之间的一组相关数据如下表所示，则下列说法错误的为

A.变量，之间呈现正相关关系B.可以预测，当时，

C.D.由表格数据可知，该回归直线必过点

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网