Question

【题目】下列说法中，正确的有_______.(写出所有正确说法的序号)

①在中，若，则；

②在中，若，则是锐角三角形；

③在中，若，则；

④若是等差数列，其前项和为，则三点共线；

⑤等比数列的前项和为，若对任意的，点均在函数(且，均为常数)的图象上，则的值为.

Answer 1

【答案】①③④⑤

【解析】

根据正弦定理及边角关系可判断①;根据正弦定理及余弦定理,可判断角为锐角,但不能判断角和角的情况,因而②错误;结合正弦定理及余弦定理可判断角为钝角,结合正切的和角公式,变形后即可判断③;根据等差数列前n项和的性质,结合两点间的斜率公式,可判断④;将点带入函数解析式,结合求得通项公式,结合等比数列的定义即可求得.

对于①,在中,若,则由大角对大边可知.设外接圆半径为,由正弦定理可知,即.所以①正确;

对于②,在中,若,由正弦定理可得,可判定角为锐角.但当角或角为钝角时也成立,因而不能说明是锐角三角形,所以②错误.

对于③,在中,若,由正弦定理可知,则,所以角为钝角.由正切和角公式可知,,

所以

所以

因为角为钝角,所以角和角必为锐角,因而,所以,所以③正确;

对于④,是等差数列,其前项和为,则由等差数列前项和公式可得,则.所以,,

由两点间斜率公式可得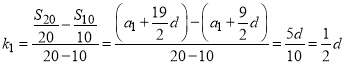

由可知三点共线,所以④正确;

对于⑤,点均在函数(且,均为常数)的图象上.

则

所以当时,

当时,

因为为等比数列,则首项也满足通项公式,所以

解得,所以⑤正确.

综上可知,正确的为①③④⑤

故答案为: ①③④⑤