题目内容
已知正项等差数列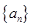 的前
的前 项和为
项和为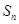 ,且满足
,且满足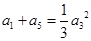 ,
,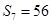 .
.
(1)求数列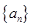 的通项公式
的通项公式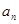 ;
;
(2)若数列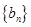 满足
满足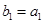 且
且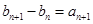 ,求数列
,求数列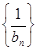 的前
的前 项和
项和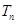 .
.
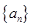 的前
的前 项和为
项和为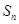 ,且满足
,且满足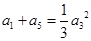 ,
,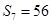 .
.(1)求数列
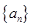 的通项公式
的通项公式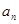 ;
;(2)若数列
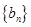 满足
满足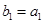 且
且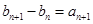 ,求数列
,求数列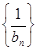 的前
的前 项和
项和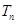 .
.(1) .(2)见解析.
.(2)见解析.
 .(2)见解析.
.(2)见解析.(1)由题意与等差数列的性质和求和公式得 ,
, ,
, ;
;
(2)根据 ,
,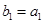 且
且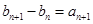 ,累加求出
,累加求出 ;
; ,裂项相消得数列
,裂项相消得数列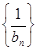 的前
的前 项和
项和 .
.
解:(1) 是等差数列且
是等差数列且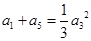 ,
, ,
,
又 .…………………………………………………2分
.…………………………………………………2分
 ,……………………………4分
,……………………………4分
 ,
, . ………………6分
. ………………6分
(2) ,
,
当 时,
时,
 ,……………………8分
,……………………8分
当 时,
时, 满足上式,
满足上式,
 ……………………………………………………10分
……………………………………………………10分

 . ………………………………………………12分
. ………………………………………………12分
 ,
, ,
, ;
;(2)根据
 ,
,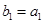 且
且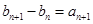 ,累加求出
,累加求出 ;
; ,裂项相消得数列
,裂项相消得数列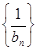 的前
的前 项和
项和 .
.解:(1)
 是等差数列且
是等差数列且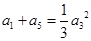 ,
, ,
,又
 .…………………………………………………2分
.…………………………………………………2分 ,……………………………4分
,……………………………4分 ,
, . ………………6分
. ………………6分(2)
 ,
,
当
 时,
时,
 ,……………………8分
,……………………8分当
 时,
时, 满足上式,
满足上式,
 ……………………………………………………10分
……………………………………………………10分
 . ………………………………………………12分
. ………………………………………………12分
练习册系列答案
相关题目
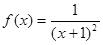 ,数列
,数列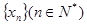 的项满足:
的项满足: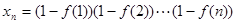 ,(1)试求
,(1)试求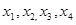
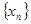 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明.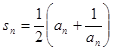 .
.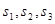 ;
;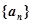 中,
中,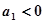 ,又
,又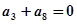 ,则使数列
,则使数列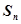 取最小值时的n的值是 。
取最小值时的n的值是 。
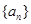 为等差数列,且
为等差数列,且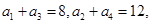 (Ⅰ)求数列
(Ⅰ)求数列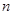 项和为
项和为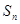 ,若
,若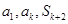 成等比数列,求正整数
成等比数列,求正整数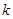 的值。
的值。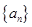 中,
中,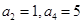 ,则
,则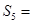
 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 、
、 、
、 成等比数列。
成等比数列。 ,求数列
,求数列 的前
的前 项和
项和 。
。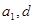 为实数,首项为
为实数,首项为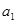 ,公差为
,公差为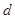 的等差数列
的等差数列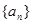 的前n项和为
的前n项和为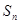 ,满足
,满足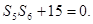
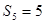 ,求
,求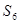 及
及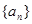 满足
满足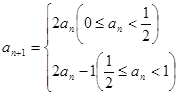 若
若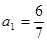 ,则
,则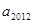 的值为:( )
的值为:( )