题目内容
17.若等式cosx•cosy=cos(x+y)成立,则x,y应满足的条件为x=kπ,或y=kπ,k∈Z.分析 由题意利用两角和的余弦公式可得sinxsiny=0,即sinx=0 或siny=0,由此求得x和y的取值范围,即为所求.
解答 解:∵cos(x+y)=cosxcosy-sinxsiny,若等式cosx•cosy=cos(x+y)成立,
则sinxsiny=0,即sinx=0 或siny=0,故x=kπ,或y=kπ,k∈Z,
故答案为:x=kπ,或y=kπ,k∈Z.
点评 本题主要考查两角和的余弦公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.定义数列{an}的“项的倒数的n倍和数”为Tn=$\frac{1}{a_1}+\frac{2}{a_2}+…+\frac{n}{a_n}(n∈{N^*})$,已知Tn=$\frac{n^2}{2}$(n∈N*),则数列{an}是( )
| A. | 单调递减的 | B. | 单调递增的 | C. | 先增后减的 | D. | 先减后增的 |
5.“φ=0”是“函数y=cos(x+φ)为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.今有一组实验数据,如表:
现准备从以下函数中选择一个最能代表两个变量x、y之间的规律,则拟合最好的是( )
| x | 1.993 | 3.002 | 4.001 | 5.032 | 6.121 |
| y | 1.501 | 4.413 | 7.498 | 12.04 | 17.93 |
| A. | y=2x-1+1 | B. | $y=\frac{3}{2}{log_2}x$ | C. | $y=\frac{1}{2}{x^2}-\frac{1}{2}$ | D. | y=-2x-2 |
6.已知命题甲:a+b≠4,命题乙:a≠1且b≠3,则命题甲是命题乙的( )
| A. | 充分必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
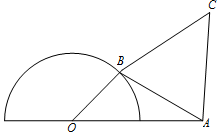 半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?
半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?