题目内容
（2013•天津）已知函数
．
（1）求f（x）的最小正周期；
（2）求f（x）在区间
上的最大值和最小值．
．（1）求f（x）的最小正周期；
（2）求f（x）在区间
上的最大值和最小值．（1）π （2）最大值为f（
）=2
；最小值为f（0）=﹣2．
）=2；最小值为f（0）=﹣2．（1）∵sinxcosx=
sin2x，cos2x=（1+cos2x）
∴f（x）=﹣
sin（2x+
）+6sinxcosx﹣2cos2x+1=﹣sin2x﹣cos2x+3sin2x﹣（1+cos2x）+1
=2sin2x﹣2cos2x=2sin（2x﹣）
因此，f（x）的最小正周期T=
=π；
（2）∵0≤x≤
，∴﹣≤2x﹣≤
∴当x=0时，sin（2x﹣
）取得最小值﹣
；当x=时，sin（2x﹣）取得最大值1
由此可得，f（x）在区间
上的最大值为f（）=2；最小值为f（0）=﹣2．
sin2x，cos2x=（1+cos2x）∴f（x）=﹣
sin（2x+）+6sinxcosx﹣2cos2x+1=﹣sin2x﹣cos2x+3sin2x﹣（1+cos2x）+1=2sin2x﹣2cos2x=2
sin（2x﹣）因此，f（x）的最小正周期T=
=π；（2）∵0≤x≤
，∴﹣≤2x﹣≤∴当x=0时，sin（2x﹣
）取得最小值﹣；当x=时，sin（2x﹣）取得最大值1由此可得，f（x）在区间
上的最大值为f（）=2；最小值为f（0）=﹣2．
练习册系列答案
备战中考寒假系列答案
相关题目
,
.
的值域是( )
是( )
的偶函数
的偶函数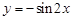 
；②
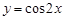；③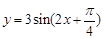
，其图象仅通过向左（或向右）平移就能与函数
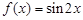的图象重合的是_____.（填上符合要求的函数对应的序号）
，且
，
，则函数
图象的一条对称轴的方程为（ ）
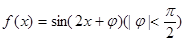的图象向左平移
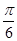个单位后关于原点对称，则函
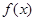在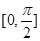
上的最小值为( )
,若
是偶函数，则
__________．