题目内容
已知以a1为首项的数列{an}满足:an+1=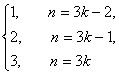
(1)当a1=1,c=1,d=3时,求数列{an}的通项公式;
(2)当0<a1<1,c=1,d=3时,试用a1表示数列{an}前100项的和S100;
(3)当0<a1<![]() (m是正整数),c=
(m是正整数),c=![]() ,正整数d≥3m时,求证:数列a2-
,正整数d≥3m时,求证:数列a2-![]() ,a3m+2-
,a3m+2-![]() ,a6m+2-
,a6m+2-![]() ,a9m+2-
,a9m+2-![]() 成等比数列当且仅当d=3m.
成等比数列当且仅当d=3m.
解:(1)由题意得an=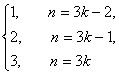 (k∈Z+).
(k∈Z+).
(2)当0<a1<1时,
a2=a1+1,a3=a1+2,a4=a1+3,a5=![]() +1,a6=
+1,a6=![]() +2,a7=
+2,a7=![]() +3,…,a3k-1=
+3,…,a3k-1=![]() +1,a3k=
+1,a3k=![]() +2,a3k+1=
+2,a3k+1=![]() +3,
+3,
∴S100=a1+(a2+a3+a4)+(a5+a6+a7)+…+(a98+a99+a100)
=a1+(3a1+6)+(a1+6)+(![]() +6)+…+(
+6)+…+(![]() +6)
+6)
=a1+a1(3+1+![]() +…+
+…+![]() )+6×33
)+6×33
=![]() (11-
(11-![]() )a1+198.
)a1+198.
(3)当d=3m时,a2=a1+![]() ,
,
∵a3m=a1+![]() =a1-
=a1-![]() +3<3<a1+3=a3m+1,
+3<3<a1+3=a3m+1,
∴a3m+2=![]() +
+![]() .
.
∵a6m=![]() -
-![]() +3<3<
+3<3<![]() +3=a6m+1,
+3=a6m+1,
∴a6m+2=![]() +
+![]() .
.
∵a9m=![]() -
-![]() +3<3<
+3<3<![]() +3=a9m+1,
+3=a9m+1,
∴a9m+2=![]() +
+![]() .
.
∴a2-![]() =a1,a3m+2-
=a1,a3m+2-![]() =
=![]() ,a6m+2-
,a6m+2-![]() =
=![]() .
.
∴a9m+2-![]() =
=![]() .
.
综上所述,当d=3m时,数列a2-![]() ,a3m+2-
,a3m+2-![]() ,a6m+2
,a6m+2![]() ,a9m+2-
,a9m+2-![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
当d≥3m+1时,a3m+2=![]() ∈(0,
∈(0,![]() ),
),
a6m+2=![]() +3∈(3,3+
+3∈(3,3+![]() ),a6m+3=
),a6m+3=![]() ∈(0,
∈(0,![]() ),
),
a9m+2=![]() +
+![]() ∈(3-
∈(3-![]() ,3),
,3),
由于a3m+2-![]() <0,a6m+2-
<0,a6m+2-![]() >0,a9m+2-
>0,a9m+2-![]() >0.
>0.
故数列a2-![]() ,a3m+2-
,a3m+2-![]() ,a6m+2-
,a6m+2-![]() ,a9m+2-
,a9m+2-![]() 不是等比数列.
不是等比数列.
所以,数列a2-![]() ,a3m+2-
,a3m+2-![]() ,a6m+2-
,a6m+2-![]() ,a9m+2-
,a9m+2-![]() 成等比数列,
成等比数列,
当且仅当d=3m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

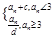
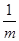 (m是正整数),c=
(m是正整数),c=