题目内容
已知以a1为首项的数列{an}满足:an+1=
(1)当a1=1,d=1,q=
时,求数列{an}的通项公式;
(2)当0<a1<1,d=1,q=
时,试用a1表示数列{an}前101项的和S101.
|
(1)当a1=1,d=1,q=
| 1 |
| 2 |
(2)当0<a1<1,d=1,q=
| 1 |
| 2 |
分析:(1)由an+1=
,a1=1,d=1,q=
,分别求出a2,a3,a4,总结规律,能求出数列{an}的通项公式.
(2)由0<a1<1,d=1,q=
,知a2=a1+1,a3=a1+2,a4=
+1,a5=
+2,a6=
+1,…,a2k=
+1,a2k+1=
+2,由此能用用a1表示数列{an}前101项的和S101.
|
| 1 |
| 2 |
(2)由0<a1<1,d=1,q=
| 1 |
| 2 |
| a1 |
| 2 |
| a1 |
| 2 |
| a1 |
| 22 |
| a1 |
| 2k-1 |
| a1 |
| 2k-1 |
解答:解:(1)∵an+1=
,a1=1,d=1,q=
,
∴a2=1+1=2,
a3=
×2=1,
a4=1+1=2,
…
∴an=
,k∈N*.
(2)当0<a1<1,d=1,q=
时,
a2=a1+1,a3=a1+2,a4=
+1,a5=
+2,a6=
+1,…,
a2k=
+1,a2k+1=
+2,
所以S101=a1+(a2+a3)+(a4+a5)+…+(a100+a101)
=a1+(2a1+3)+(a1+3)+(
+3)+…+(
+3)
=a1+
+50×3=a1[5-(
)48]+150.
|
| 1 |
| 2 |
∴a2=1+1=2,
a3=
| 1 |
| 2 |
a4=1+1=2,
…
∴an=
|
(2)当0<a1<1,d=1,q=
| 1 |
| 2 |
a2=a1+1,a3=a1+2,a4=
| a1 |
| 2 |
| a1 |
| 2 |
| a1 |
| 22 |
a2k=
| a1 |
| 2k-1 |
| a1 |
| 2k-1 |
所以S101=a1+(a2+a3)+(a4+a5)+…+(a100+a101)
=a1+(2a1+3)+(a1+3)+(
| a1 |
| 2 |
| a1 |
| 248 |
=a1+
2a1[1-(
| ||
1-
|
| 1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,仔细解答,注意递推公式的灵活运用.

练习册系列答案
相关题目

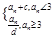
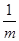 (m是正整数),c=
(m是正整数),c=