题目内容
10.已知函数$f(x)=\frac{{\sqrt{3}}}{2}sin2x+\frac{1}{2}cos2x$.(Ⅰ)求函数f(x)的最小正周期T和单调增区间;
(Ⅱ)若$x∈[0,\frac{π}{2}]$,求f(x)的最大值和最小值.
分析 由三角函数公式化简可得f(x)=sin(2x+$\frac{π}{6}$),
(Ⅰ)由周期公式可得最小正周期,解$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$可得单调增区间;
(Ⅱ)由$x∈[0,\frac{π}{2}]$可得$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$,易得三角函数的最值.
解答 解:由三角函数公式化简可得$f(x)=\frac{{\sqrt{3}}}{2}sin2x+\frac{1}{2}cos2x=sin(2x+\frac{π}{6})$,
(Ⅰ)由周期公式可得函数f(x)的最小正周期$T=\frac{2π}{2}=π$,
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$可得$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ(k∈Z)$,
∴函数f(x)的单调增区间为$[-\frac{π}{3}+kπ,\frac{π}{6}+kπ](k∈Z)$;
(Ⅱ)∵$x∈[0,\frac{π}{2}]$,∴$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$,
∴当$2x+\frac{π}{6}=\frac{π}{2}$时,$f{(x)_{max}}=sin\frac{π}{2}=1$,
当$2x+\frac{π}{6}=\frac{7π}{6}$时,$f{(x)_{min}}=sin\frac{7π}{6}=-\frac{1}{2}$.
点评 本题考查三角函数恒等变换,涉及三角函数单调性和最值以及周期性,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.若α是第二象限角,则$\frac{α}{2}$是第( )象限角.
| A. | 二、三 | B. | 一、二 | C. | 二、四 | D. | 一、三 |
20.若函数f(x)=x•ex-m在R上存在两个不同的零点,则m的取值范围是( )
| A. | $-\frac{1}{e}<m<0$ | B. | $m>-\frac{1}{e}$ | C. | m>e | D. | -e<m<0 |
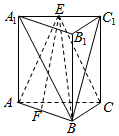 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,$A{A_1}=AC=2,AB=\sqrt{3}$,E,F分别是A1C1,AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,$A{A_1}=AC=2,AB=\sqrt{3}$,E,F分别是A1C1,AB的中点.