题目内容
已知点P(t,y)在函数f(x)=求证:(1)|ac|≥4;
(2)在(-1,+∞)上f(x)单调递增.
(3)f(|a|)+f(|c|)>1.
证明:(1)∵t∈R,t≠-1,∴Δ=(-c
∵c≠0,∴c
(2)由f(x)=1-![]() ,
,
证法一:设 ,则f(x2)-f(x1)=1-
,则f(x2)-f(x1)=1-![]() -1+
-1+![]() +1=
+1=![]() .
.
∵ ,
,
∴x2-x1>0,x1+1>0,x2+1>0.
∴f(x2)-f(x1)>0,即f(x2)>f(x1).
∴x>-1时,f(x)单调递增.
证法二:由f′(x)=![]() ,x≠-1,得f′(x)>0.
,x≠-1,得f′(x)>0.
∴x>-1时,f(x)单调递增.
(3)∵f(x)在x>-1时单调递增,|c|≥![]() >0.
>0.
∴f(|c|)≥f(![]() )=
)= ,
,
f(|a|)+f(|c|)≥![]() =1.
=1.
∴f(|a|)+f(|c|)>1.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
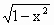 图象上的动点,过点P作此函数图象的切线,切线斜率k是点P横坐标t的函数,记为k=f(t),则函数k=f(t)在(-1,1)上是
图象上的动点,过点P作此函数图象的切线,切线斜率k是点P横坐标t的函数,记为k=f(t),则函数k=f(t)在(-1,1)上是