Question

若点（

2

，2）在幂函数f（x）的图象上，点（-2，

1

4

）在幂函数g（x）的图象上，问当x为何值时，（1）f（x）＞g（x）；（2）f（x）=g（x）；（3）f（x）＜g（x）．

Answer 1

分析：求函数f（x），g（x）的解析式，由于已知两函数是幂函数，故可用待定系数法设出两函数的解析式，代入点的坐标求出函数的解析式．由于两个函数在第一象限一个是减函数一个是增函数，故可令两者相等，解出它们的交点坐标，再由函数的单调性得出f（x）＜g（x）的解集，由于两函数都是偶函数，可由对称性得出函数在（-∞，0）上的解集，取两者的并集即得不等式f（x）＜g（x）的解集，即得所求的x的取值范围．对于f（x）＞g（x）同样可以利用图象法求解．

解答：解：设f（x）=x^α，由点（

2

，2）在幂函数f（x）的图象上，得(

2

)α=2，
∴α=2，则f（x）=x² ，同理得g（x）=x^-2
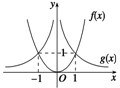
在同一坐标系中作出这两个函数的图象，如图所示．
观察图象可得：
（1）当x＞1或x＜-1时，f（x）＞g（x）；
（2）当x=1或x=-1时，f（x）=g（x）；
（3）当-1＜x＜1，且x≠0时，f（x）＜g（x）．

点评：本题考查了用待定系数法求函数解析式、函数图象交点、幂函数的概念、解析式、定义域、值域等知识．考查数形结合思想，属于基础题．