题目内容
设函数f(x)=
,则f(
)的值为 .
|
| 1 |
| f(2) |
考点:分段函数的应用
专题:函数的性质及应用
分析:直接利用分段函数,求出f(2),然后求解所求表达式的值.
解答:
解:函数f(x)=
,则f(2)=22-2=2
f(
)=f(
)=1-(
)2=
.
故答案为:
.
|
f(
| 1 |
| f(2) |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查分段函数的应用,函数的值的求法,考查计算能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知实数x,y满足
,则z=x+y的最小值等于( )
|
| A、0 | B、1 | C、2 | D、3 |
当0<x<1,函数y=x(1-x)的最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
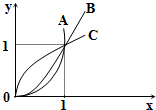 已知幂函数①y=x
已知幂函数①y=x | 1 |
| 2 |
| A、①②③ | B、③①② |
| C、③②① | D、①③② |
三个数70.8,0.87,log0.87的大小顺序是( )
| A、0.87<log0.87<70.8 |
| B、0.87<70.8<log0.87 |
| C、log0.87<70.8<0.87 |
| D、log0.87<0.87<70.8 |