题目内容
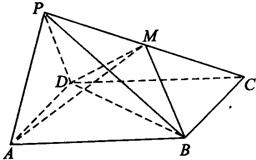（2010•济南一模）如图，在四棱锥P-ABCD中，侧面PAD是正三角形，且垂直于底面ABCD，底面ABCD是边长为2的菱形，∠BAD=60°，M为PC上一点，且PA∥平面BDM，（1）求证：M为PC的中点；
（2）求证：面ADM⊥面PBC．
分析：（1）连接AC，AC与BD交于G，根据线面平行的性质可知PA∥MG，而底面ABCD为菱形，则G为AC的中点，从而MG为△PAC的中位线，最终说明M为PC的中点．
（2）取AD中点O，连接PO，BO．分别以OA，OB，OP为x、y、z轴，建立空间直角坐标系，根据
•
=0，
•
=0可得DM⊥BP，DM⊥CB，再根据线面垂直的判定定理可知DM⊥平面PBC，又DM?平面ADM，满足面面垂直的判定定理所需条件．
（2）取AD中点O，连接PO，BO．分别以OA，OB，OP为x、y、z轴，建立空间直角坐标系，根据
| DM |
| BP |
| DM |
| CB |
解答：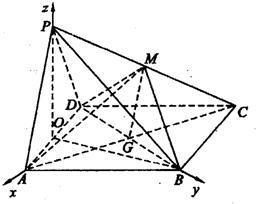
证明：
（1）连接AC，AC与BD交于G，则面PAC∩面BDM=MG，
由PA∥平面BDM，可得PA∥MG（3分）
∵底面ABCD为菱形，∴G为AC的中点，
∴MG为△PAC的中位线．
因此M为PC的中点．（5分）
（2）取AD中点O，连接PO，BO．
∵△PAD是正三角形，∴PO⊥AD，又因为平面PAD⊥平面ABCD，
所以，PO⊥平面ABCD，（7分）
∵底面ABCD是菱形且∠BAD=60°，△ABD是正三角形，
∴AD⊥OB．
∴OA，OB，OP两两垂直，建立空间直角坐标系{
，
，
}（7分）
则A（1，0，0），B(0，
，0)，D(-1，0，0)，P(0，0，
)
∴
=(1，0，
)，
=(-1，
，0)
∴
=
(
+
)=
(
+
)=(0，
，
)（9分）
=(0，-
，
)，
=
=（2，0，0）
∴
•
=0-
+
=0，
•
=0+0+0=0
∴DM⊥BP，DM⊥CB（11分）
∴DM⊥平面PBC，又DM?平面ADM，
∴面ADM⊥面PBC（12分）
证明：（1）连接AC，AC与BD交于G，则面PAC∩面BDM=MG，
由PA∥平面BDM，可得PA∥MG（3分）
∵底面ABCD为菱形，∴G为AC的中点，
∴MG为△PAC的中位线．
因此M为PC的中点．（5分）
（2）取AD中点O，连接PO，BO．
∵△PAD是正三角形，∴PO⊥AD，又因为平面PAD⊥平面ABCD，
所以，PO⊥平面ABCD，（7分）
∵底面ABCD是菱形且∠BAD=60°，△ABD是正三角形，
∴AD⊥OB．
∴OA，OB，OP两两垂直，建立空间直角坐标系{
| OA |
| OB |
| OP |
则A（1，0，0），B(0，
| 3 |
| 3 |
∴
| DP |
| 3 |
| AB |
| 3 |
∴
| DM |
| 1 |
| 2 |
| DP |
| DC |
| 1 |
| 2 |
| DP |
| AB |
| ||
| 2 |
| ||
| 2 |
| BP |
| 3 |
| 3 |
| CB |
| DA |
∴
| DM |
| BP |
| 3 |
| 2 |
| 3 |
| 2 |
| DM |
| CB |
∴DM⊥BP，DM⊥CB（11分）
∴DM⊥平面PBC，又DM?平面ADM，
∴面ADM⊥面PBC（12分）
点评：本题主要考查平面与平面垂直的判定，以及线面平行的性质和利用向量法证明立体几何的有关问题，同时考查了空间想象能力，计算能力和推理能力，以及转化与划归的思想，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
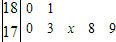（2010•济南一模）一次选拔运动员，测得7名选手的身高（单位cm）分布茎叶图如图，记录的平均身高为177cm，有一名候选人的身高记录不清楚，其末位数记为x，那么x的值为（ ）