题目内容
12.已知a,b,c∈R+,求证:2(a3+b3+c3)≥a(b2+c2)+b(c2+a2)+c(a2+b2).分析 运用作差法,证明a3+b3-a2b-ab2≥0,即有a3+b3≥a2b+ab2;同理可得b3+c3≥b2c+bc2;a3+c3≥a2c+ac2.再由累加法,即可得证.
解答 证明:由a,b,c∈R+,
a3+b3-a2b-ab2=(a+b)(a2-ab+b2)-ab(a+b)
=(a+b)(a2-2ab+b2)
=(a+b)(a-b)2≥0,
即有a3+b3≥a2b+ab2;
同理可得b3+c3≥b2c+bc2;
a3+c3≥a2c+ac2.
上面三式,相加可得,
2(a3+b3+c3)≥a2b+ab2+b2c+bc2+a2c+ac2
=a(b2+c2)+b(c2+a2)+c(a2+b2),
当且仅当a=b=c时,取得等号.
点评 本题考查不等式的证明,考查作差法和累加的应用,考查运算能力,属于基础题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
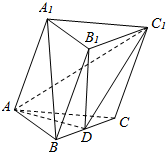 如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.
如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.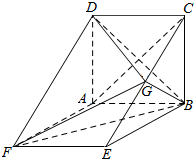 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD上平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD上平面ABEF,G为EC的中点.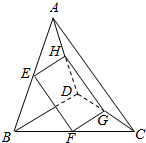 如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.