题目内容
已知直线l:x=my+1过椭圆 的右焦点F,抛物线
的右焦点F,抛物线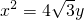 的焦点为椭圆C的上顶点,且直线l交椭圆C于A,B两点,点A,F,B在直线x=4上的射影依次为点D,K,E.
的焦点为椭圆C的上顶点,且直线l交椭圆C于A,B两点,点A,F,B在直线x=4上的射影依次为点D,K,E.
(1)求椭圆C的方程;
(2)若直线l交y轴于点M,且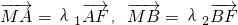 ,当m变化时,证明:
,当m变化时,证明: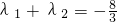 ;
;
(3)连接AE,BD,试探索当m变化时,直线AE与BD是否相交于定点?若是,求出定点的坐标,并给出证明;否则,请说明理由.
(1)解:椭圆右焦点F(1,0),∴c=1,
抛物线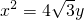 的焦点坐标(0,
的焦点坐标(0, ),∴b=
),∴b=
∴b2=3
∴a2=b2+c2=4
∴椭圆C: …(3分)
…(3分)
(2)证明:由题意,m≠0,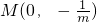 ,设A(x1,y1),B(x2,y2)
,设A(x1,y1),B(x2,y2)
由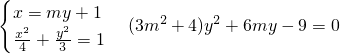 ,∴△=(6m)2+36(3m2+4)=144(m2+1)>0
,∴△=(6m)2+36(3m2+4)=144(m2+1)>0
∴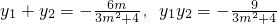 …(6分)
…(6分)
又由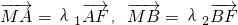 得:
得: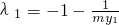 ,
,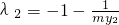
∴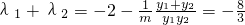 …(8分)
…(8分)
(3)解:m=0时,得N( ,0),猜想:m变化时,直线AE与BD相交于定点N(
,0),猜想:m变化时,直线AE与BD相交于定点N( ,0),
,0),
由(2)知A(x1,y1),B(x2,y2)于是 D(4,y1),E(4,y2),
先证直线AE过定点N:直线AE的方程为: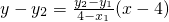
当x= 时
时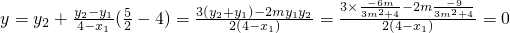
所以,点N在直线AE上,同理可得点N在直线BD上.
即m变化时,直线AE与BD相交于定点N( ,0)…(13分)
,0)…(13分)
分析:(1)由题设条件能够求出c、b=,从而求出椭圆C的方程;
(2)直线l与椭圆联立方程组,由根与系数的关系,结合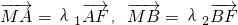 ,即可证得结论;
,即可证得结论;
(3)由题设条件证明点N( ,0)在既直线AE上,又在直线BD上,即可得到结论.
,0)在既直线AE上,又在直线BD上,即可得到结论.
点评:本题是椭圆的综合应用题,有一定的难度.考查椭圆的标准方程,直线与椭圆的位置关系以及直线和直线之间的关系等基础知识,考查推理论证能力,运算求解能力.
抛物线
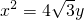 的焦点坐标(0,
的焦点坐标(0, ),∴b=
),∴b=
∴b2=3
∴a2=b2+c2=4
∴椭圆C:
 …(3分)
…(3分)(2)证明:由题意,m≠0,
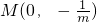 ,设A(x1,y1),B(x2,y2)
,设A(x1,y1),B(x2,y2)由
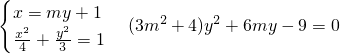 ,∴△=(6m)2+36(3m2+4)=144(m2+1)>0
,∴△=(6m)2+36(3m2+4)=144(m2+1)>0∴
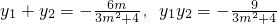 …(6分)
…(6分)又由
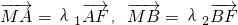 得:
得: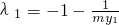 ,
,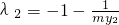
∴
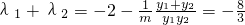 …(8分)
…(8分)(3)解:m=0时,得N(
 ,0),猜想:m变化时,直线AE与BD相交于定点N(
,0),猜想:m变化时,直线AE与BD相交于定点N( ,0),
,0),由(2)知A(x1,y1),B(x2,y2)于是 D(4,y1),E(4,y2),
先证直线AE过定点N:直线AE的方程为:
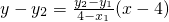
当x=
 时
时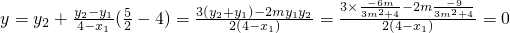
所以,点N在直线AE上,同理可得点N在直线BD上.
即m变化时,直线AE与BD相交于定点N(
 ,0)…(13分)
,0)…(13分)分析:(1)由题设条件能够求出c、b=,从而求出椭圆C的方程;
(2)直线l与椭圆联立方程组,由根与系数的关系,结合
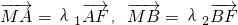 ,即可证得结论;
,即可证得结论;(3)由题设条件证明点N(
 ,0)在既直线AE上,又在直线BD上,即可得到结论.
,0)在既直线AE上,又在直线BD上,即可得到结论.点评:本题是椭圆的综合应用题,有一定的难度.考查椭圆的标准方程,直线与椭圆的位置关系以及直线和直线之间的关系等基础知识,考查推理论证能力,运算求解能力.

练习册系列答案
相关题目
 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2. (2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).
(2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0). 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: