题目内容
已知函数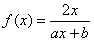 ,f(1)=1,
,f(1)=1,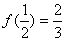 ,令x1=
,令x1=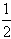 ,xn+1=f(xn)。
,xn+1=f(xn)。
(1)求数列{xn}的通项公式;
(2)证明x1x2x3…xn>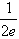 。
。
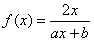 ,f(1)=1,
,f(1)=1,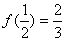 ,令x1=
,令x1=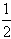 ,xn+1=f(xn)。
,xn+1=f(xn)。(1)求数列{xn}的通项公式;
(2)证明x1x2x3…xn>
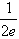 。
。解:由f(1)=1,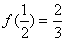 得a=b=1,
得a=b=1,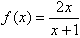 。
。
(1)先求出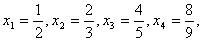
猜想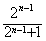
用数学归纳法证明
当n=1显然成立;
假设n=k成立,即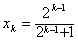
则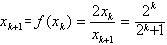 得证。
得证。
(2)我们证明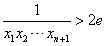 ,事实上
,事实上
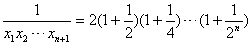
我们注意到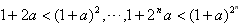
于是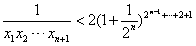
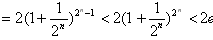
∴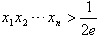 。
。
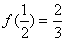 得a=b=1,
得a=b=1,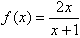 。
。(1)先求出
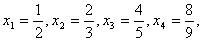
猜想
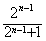
用数学归纳法证明
当n=1显然成立;
假设n=k成立,即
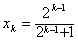
则
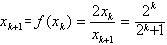 得证。
得证。(2)我们证明
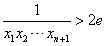 ,事实上
,事实上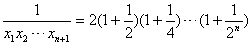
我们注意到
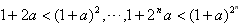
于是
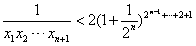
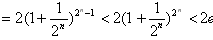
∴
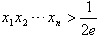 。
。
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 那么f(-1)+f(1)= .
那么f(-1)+f(1)= .