Question

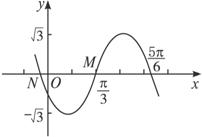
下图为y=Asin(ωx+φ)的图象的一段，求其解析式.

Answer 1

解析一:以点N为第一个零点，则A=-,T=2(-)=π,

∴ω=2，此时解析式为y=-sin(2x+φ).

∵点N(-，0),

∴-×2+φ=0φ=.∴所求解析式为y=-sin(2x+).                       ①

解析二:以点M(，0)为第一个零点，则A=,ω==2，解析式为y=sin(2x+φ)，将点M的坐标代入得2×+φ=0φ=-,

∴所求解析式为y=sin(2x-).                                             ②

点评：(1)①与②是一致的，由①可得②，事实上y=-sin(2x+)=-sin(2x+π-)=3sin(2x-)，同样由②也可得①.

(2)由此题的两种解法可见，在由图象求解析式时，“第一个零点”的确定是重要的，应尽量使A取正值.若以N点为五点法作图中的第一个零点，由于此时曲线是先下降后上升(类似于y=-sinx的图象),所以A＜0；若以M点为第一个零点，由于此时曲线是先上升后下降(类似于y=sinx的图象),所以A＞0.

(3)由图象求解析式通常采用两种方法确定系数ω、φ.①如果图象明确指出了周期T的大小和初始值x₀(第一个零点的横坐标),可以直接解出ω和φ，这里ω=，φ=-ωx₀.②代入点的坐标，通过解最简单的三角方程，再结合图形确定ω和φ.