题目内容
（本小题满分14分）如图, 在矩形
中,
,
分别为线段
的中点, 
⊥平面.
(1) 求证:
∥平面
；
(2) 求证:平面
⊥平面
；
(3) 若
, 求三棱锥
的
体积.
中, , 分别为线段的中点, ⊥平面.(1) 求证:
∥平面；(2) 求证:平面
⊥平面；(3) 若
, 求三棱锥的体积.
证明:⑴ 在矩形ABCD中,
∵AP＝PB, DQ＝QC,
∴AP
CQ.
∴AQCP为平行四边形.-------------2分
∴CP∥AQ.
∵CP
平面CEP,
AQ
平面CEP,
∴AQ∥平面CEP. ----------------4分
⑵ ∵EP⊥平面ABCD,
AQ平面ABCD,
∴AQ⊥EP. ----------------------6分
∵AB＝2BC, P为AB中点, ∴AP＝AD. 连PQ, ADQP为正方形.
∴AQ⊥DP.-----------------------------------------8分
又EP∩DP＝P, ∴AQ⊥平面DEP.
∵AQ平面AEQ. ∴平面AEQ⊥平面DEP. -----------------------10分
⑶解：∵⊥平面
∴EP为三棱锥的高
所以
-----------------------------14分
∵AP＝PB, DQ＝QC,
∴AP
CQ. ∴AQCP为平行四边形.-------------2分
∴CP∥AQ.
∵CP
平面CEP, AQ
平面CEP,∴AQ∥平面CEP. ----------------4分
⑵ ∵EP⊥平面ABCD,
AQ
平面ABCD,∴AQ⊥EP. ----------------------6分
∵AB＝2BC, P为AB中点, ∴AP＝AD. 连PQ, ADQP为正方形.
∴AQ⊥DP.-----------------------------------------8分
又EP∩DP＝P, ∴AQ⊥平面DEP.
∵AQ
平面AEQ. ∴平面AEQ⊥平面DEP. -----------------------10分 ⑶解：∵
⊥平面∴EP为三棱锥
的高所以
-----------------------------14分
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
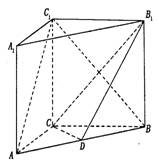
的棱长为
，过点
作平面
的垂线，垂足为点
，则以下命题中，错误的命题是（ ）
的垂心
垂直平面
所成角为
的长度分别等于
、
，每条弦的两端都在球面上运动，则两弦中点之间距离的最大值为 ．
⊙O所在的平面，
是⊙O的直径，
，
C是⊙O上一点，且
，
与⊙O所在的平面成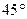
角，
是
；(Ⅱ) 求证：
；
和
，
、
分别为
、
的中点，每两条弦的两端都在球面上运动，有下面四个命题：①弦
的最大值为5 ④
的经线上有A、B两点，A在北纬
，则它们的球面距离是__________.