题目内容
如图,α-l-β是120°的二面角,A、B两点在二面角的棱l上,AB=2,D在α内,△ABD是等腰直角三角形,且∠DAB=90°,C在β内,△ABC为等腰直角三角形,且∠ACB=90°.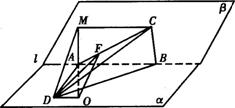
(1)求异面直线AB、CD所成角;
(2)求二面角D-AC-B的大小.
解:(1)过C作CM∥l,过A作AM⊥l

且AM∩CM=M
即∠DCM为异面直线AB与CD所成角.
∵△DAM为直角三角形∠DAB=90°
∴∠MAD=120°
由已知AC=![]()
![]() AM=1=CM
AM=1=CM
∴DM=![]()
∴tan∠DCM=![]()
即AB与CD所成角是arctan![]() .
.
(2)过D作DO⊥MA于O(实际为MA延长线于O)易得DO⊥β,过O作DF⊥AC于F,连DF
∴∠DFO为二面角D-AC-B的平面角
∵DO=DAsin60°=![]() ,OA=1
,OA=1
OF=OAsin45°=![]() 在Rt△DOF中,
在Rt△DOF中,
tan∠FDO=
∴二面角D-AC-B的大小为arctan![]()

练习册系列答案
相关题目
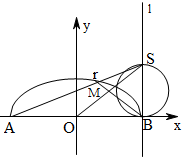 已知A,B 分别为曲线C:
已知A,B 分别为曲线C:
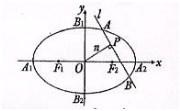 如图,椭圆C2
如图,椭圆C2 如图,椭圆
如图,椭圆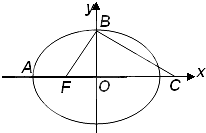 (2009•泰安一模)如图,点F是椭圆
(2009•泰安一模)如图,点F是椭圆