题目内容
|
 且
且
(Ⅰ)求k的值;
(Ⅱ)求
(文)某村计划建造一个室内面积为800m2的矩形蔬菜温室. 在温室内,种植蔬菜时需要沿左、右两侧与前侧内墙各保留1m宽的空地作为通道,后侧内墙不留空地(如图所示),问当温室的长是多少米时,能使蔬菜的种植面积最大?
|
【答案】
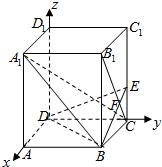
(理)解:(Ⅰ)∵正方体OABC—O′A′B′C′的棱长为2,且N、Q分别为BB′、
OO′的中点,AM=k,
∴Q(0,0,1),M(2,0,k),N(2,2,1) ………………2分
∴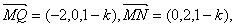
又∵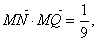 ………………4分
………………4分
∴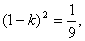
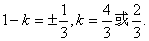 ∵
∵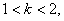 ∴
∴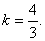
(Ⅱ)∵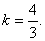 ………………6分
………………6分
∴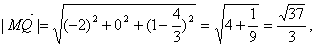 ………………8分
………………8分
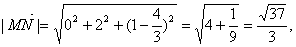 ………………10分
………………10分
∴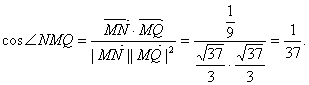 ………………12分
………………12分
(文)解:设温室的长为xm,则宽为 m(x>0) …………2分
m(x>0) …………2分
则可种植蔬菜的面积
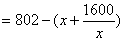 …………4分
…………4分
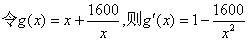 …………6分
…………6分
令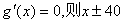 …………8分
…………8分
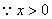
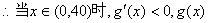 为减函数,
为减函数,
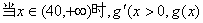 为增函数 …………10分
为增函数 …………10分
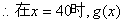 取得最小值,S(x)取得最大值
取得最小值,S(x)取得最大值
答:温室的长为40m时,蔬菜的种植面积最大. …………12分

练习册系列答案
相关题目


 (文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).
(文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).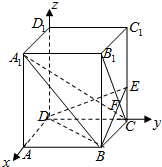 (文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).
(文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).