题目内容
如图，在空间四边形SABC中，AC、BS为其对角线，O为△ABC的重心，试证：（1）
| OA |
| OB |
| OC |
| 0 |
（2）
| SO |
| 1 |
| 3 |
| SA |
| SB |
| SC |
分析：（1）由O是△ABC的重心，表示出
、
与
，求和即可．
（2）分别用
、
，
、
，
、
表示出
，求和即得结论．
| OA |
| OB |
| OC |
（2）分别用
| SA |
| AO |
| SB |
| BO |
| SC |
| CO |
| SO |
解答：证明：（1）∵O为△ABC的重心，
∴
=-
（
+
），①
=-
（
+
），②
=-
（
+
），③
∴①+②+③得：
+
+
=-
（
+
）-
（
+
）-
（
+
）=
．
（2）∵
=
+
，④
=
+
，⑤
=
+
，⑥
且由（1）得：
+
+
=
．
∴④+⑤+⑥得：3
=（
+
）+（
+
）+（
+
）=
+
+
，
即SO=
（
+
+
）．
∴
| OA |
| 1 |
| 3 |
| AB |
| AC |
| OB |
| 1 |
| 3 |
| BA |
| BC |
| OC |
| 1 |
| 3 |
| CA |
| CB |
∴①+②+③得：
| OA |
| OB |
| OC |
| 1 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| BA |
| BC |
| 1 |
| 3 |
| CA |
| CB |
| 0 |
（2）∵
| SO |
| SA |
| AO |
| SO |
| SB |
| BO |
| SO |
| SC |
| CO |
且由（1）得：
| AO |
| BO |
| CO |
| 0 |
∴④+⑤+⑥得：3
| SO |
| SA |
| AO |
| SB |
| BO |
| SC |
| CO |
| SA |
| SB |
| SC |
即SO=
| 1 |
| 3 |
| SA |
| SB |
| SC |
点评：本题考查了空间向量的基本运算问题，是基础题．
练习册系列答案
相关题目
如图：在空间四边形ABCD中，AC=AD，BC=BD，且E是CD的中点．
如图，在空间四边形ABCD中，M，N分别是线段AB，AD上的点，若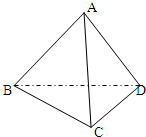
（文科做）已知：如图，在空间四边形ABCD中，AB⊥CD且AC⊥BD，求证：AD⊥BC．
如图，在空间四边形OABC中，已知E是线段BC的中点，G为AE的中点，若
如图，在空间四边形ABCD中，E，F分别是AB，CD的中点．