题目内容
求当函数y=sin2x+acosx-
a-
的最大值为1时a的值.
| 1 |
| 2 |
| 3 |
| 2 |
分析:先通过变形化为关于cosx的二次函数,配方后,根据函数式的特点,对a进行分类讨论.
解答:解:∵y=1-cos2x+acosx-
a-
=-cos2x+acosx-
-
,设cosx=t,∵-1≤cosx≤1,∴-1≤t≤1.
∴y=-t2+at-
-
=-(t-
)2+
-
-
,-1≤t≤1,函数y的对称轴为t=
.
(1)当
<-1,即a<-2时,t=-1,y有最大值-
a-
.
由已知条件可得-
a-
=1,∴a=-
>-2(舍去).
(2)当-1≤
≤1时,即-2≤a≤2时,t=
,y有最大值
-
-
.
由已知条件可得
-
-
=1,解得a=1-
或a=1+
(舍去).
(3)当
>1,即a>2时,则当t=1,y有最大值
-
.
由已知条件可得
-
=1,∴a=5.
综上可得,a=1-
或a=5.
| 1 |
| 2 |
| 3 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
∴y=-t2+at-
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
(1)当
| a |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
由已知条件可得-
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 3 |
(2)当-1≤
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
由已知条件可得
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
| 7 |
| 7 |
(3)当
| a |
| 2 |
| a |
| 2 |
| 3 |
| 2 |
由已知条件可得
| a |
| 2 |
| 3 |
| 2 |
综上可得,a=1-
| 7 |
点评:本题主要考查同角三角函数的基本关系,二次函数的性质应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.
sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.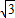 sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.
sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围. sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.
sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.