题目内容
知函数y=sin2ωx+
sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.
| 3 |
分析:利用二倍角公式以及两角和的正弦函数,化简函数为一个角的一个三角函数的形式,通过函数的周期公式求出ω,通过x 的范围,求出相位的范围,然后求出函数的值的范围.
解答:解:y=
(1-cos2ωx)+
sin2ωx-1…(4分)(每个公式的应用得2分)
=sin(2ωx-
)-
…(6分)
因为T=
=2π,所以ω=
…(8分)
y=sin(x-
)-
…(9分)
因为0≤x≤π,所以-
≤x-
≤
…(10分)
-
≤sin(x-
)≤1…(12分)
故 -1≤y≤
…(14分)
| 1 |
| 2 |
| ||
| 2 |
=sin(2ωx-
| π |
| 6 |
| 1 |
| 2 |
因为T=
| 2π |
| 2ω |
| 1 |
| 2 |
y=sin(x-
| π |
| 6 |
| 1 |
| 2 |
因为0≤x≤π,所以-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
-
| 1 |
| 2 |
| π |
| 6 |
故 -1≤y≤
| 1 |
| 2 |
点评:本题是基础题,考查三角函数的化简求值,函数的周期公式的应用,考查计算能力.

练习册系列答案
相关题目
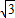 sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.
sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围. sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.
sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围. sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.
sinωxcosωx-1(ω>0)周期为2π.求:当x∈[0,π]时y的取值范围.