Question

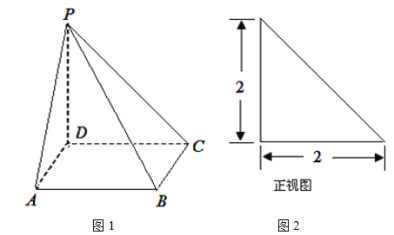
【题目】如图1，四棱锥的底面是正方形，垂直于底面，已知四棱锥的正视图，如图2所示.

（I）若M是的中点，证明：平面；

（II）求棱锥的体积.

Answer 1

【答案】（I）证明见解析；（II）.

【解析】

(Ⅰ)由正视图可知，先证明平面得到.由等腰三角形可得，利用线面垂直的判定定理可得结果； (Ⅱ)在平面PCD内过M作交CD于N，可得棱锥的体积，结合棱锥的体积等于棱锥的体积，从而可得结果.

(Ⅰ)由正视图可知，

∵PD⊥平面ABCD，∴ PD⊥BC

又∵ABCD是正方形，∴BC⊥CD.

∵，∴BC⊥平面PCD

∵平面PCD，∴DM⊥BC.

又是等腰三角形，E是斜边PC的中点，所以∴DM⊥PC

又∵，∴DM⊥平面PBC.

(Ⅱ)在平面PCD内过M作MN//PD交CD于N，所以且平面ABCD，所以棱锥M－ABD的体积为

又∵棱锥A－BDM的体积等于棱锥M－ABD的体积，

∴棱锥A－BDM的体积等于.