题目内容
 如图,已知点A(0,
如图,已知点A(0,| 1 | 4 |
分析:根据积分的几何意义求出阴影部分的面积,结合三角形面积公式建立方程关系即可求解结论.
解答:解:∵点P(x0,y0)(x0>0)在曲线y=x2上,
∴y0=x02,
则三角形△OAP面积S=
|OA||x0|=
×
x0=
x0,
阴影部分的面积为
x2dx=
x3
=
,
∵阴影部分面积与△OAP面积相等时,
∴
=
x0,
即
=
,
∴x0=
=
,
故答案为:
.
∴y0=x02,
则三角形△OAP面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
阴影部分的面积为
| ∫ | x0 0 |
| 1 |
| 3 |
| | | x0 0 |
| 1 |
| 3 |
| x | 3 0 |
∵阴影部分面积与△OAP面积相等时,
∴
| 1 |
| 3 |
| x | 3 0 |
| 1 |
| 8 |
即
| x | 2 0 |
| 3 |
| 8 |
∴x0=
|
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题主要考查积分的几何意义,利用积分求出阴影部分的面积是解决本题的关键,要求熟练掌握常见函数的积分公式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
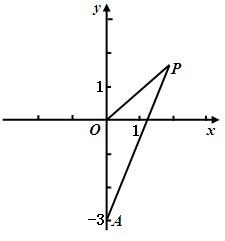 如图,已知点A(0,-3),动点P满足|PA|=2|PO|,其中O为坐标原点.
如图,已知点A(0,-3),动点P满足|PA|=2|PO|,其中O为坐标原点. 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.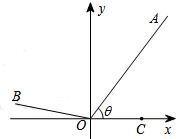 如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.
如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高. 如图,已知点A(11,0),直线x=t(-1<t<11)与函数
如图,已知点A(11,0),直线x=t(-1<t<11)与函数