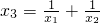Question

曲线y=ax²与直线y=kx+b相交于两点，它们的横坐标为x₁、x₂，而x₃是直线与x轴交点的横坐标，那么（　　）

• A．x₃=x₁+x₂
• B．x3=

  1

  x1

  +

  1

  x2

• C．x₁x₃=x₂x₃+x₁x₂
• D．x₁x₂=x₂x₃+x₃x₁

Answer 1

分析：联立直线与曲线方程

y=kx+b y=ax2

可得ax²-kx-b=0则可得，x1+ x2 =

k

a

，x1x2=

-b

a

，而x3=-

b

k

=-

-b a

k a

可求

解答：解：联立直线与曲线方程

y=kx+b y=ax2

可得ax²-kx-b=0
则可得，x1+ x2 =

k

a

，x1x2=

-b

a

，
x3=-

b

k

=

- b a

k a

=

x1x2

x1+x2

∴x₁x₂=x₁x₃+x₂x₃
故选D．

点评：本题主要考查了直线与曲线方程的相交的位置关系的应用，体现了方程的根与系数的关系的思想的应用．